|
Schlussrechnen und lineare Funktionen
Geradenscharen mit Derive |
|
 |
|
 |
|
 |
|
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Mögliche Vorübungen
|
|
Ihr könnt euch zunächst im "Kurs Derive: lineare Funktionen zeichnen" informieren, wie lineare Funktionen in Derive eingegeben und gezeichnet werden.
Die folgenden Abbildungen zeigen immer nur einen Ausschnitt aus den vertikal angeordneten Grafik- und Algebra-Fenstern von Derive. |
| |
|
|
Experimente mit den Funktionsgleichungen
linearer Funktionen
f(x) = mx + b
|
|
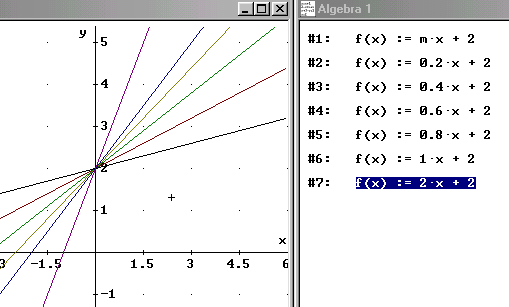
1. Erzeugt zur Übung - wie im Crash-Kurs beschrieben - eine Schar von Geraden mit konstantem y- Achsenabschnitt (b=2) und immer wieder anderer Steigung a (0,2; 0,4; 0,6; 0,8; 1; 2). Siehe die folgende Abbildung.
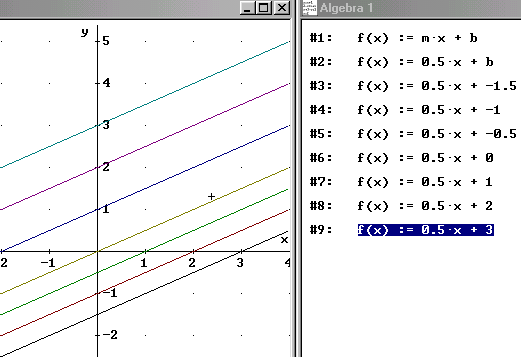
2. Erzeugt sodann eine Schar von Geraden mit konstanter Steigung a und variablem y- Achsenabschnitt b. Siehe übernächste Abbildung. |
| |
|
|
|
|
|
| |
|
|
|
|
 |
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
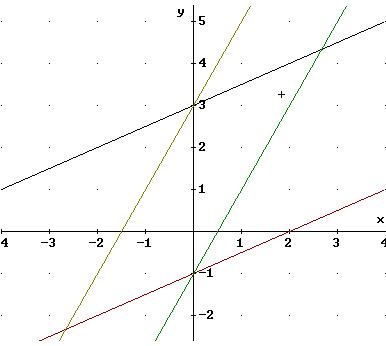
- Findet die Funktionsgleichungen der Geraden, die in der folgenden Abbildung zu sehen sind.
- Gebt euch sodann irgendeine lineare Funktionsgleichung vor und zeichnet die zugehörige Gerade g.
|
| |
|
 |
| |
|
|
| |
|
- Experimentiert
nun mit Derive ...
a) wie die Gleichung lautet, deren Gerade parallel zu g verläuft
b) wie die Gleichung lautet, deren Gerade einerseits parallel zu g verläuft und durch den Punkt (1/1) verläuft
c) wie die Gleichung lautet, deren Gerade senkrecht auf g steht und
d) wie die Gleichung lautet, deren Gerade einerseits senkrecht auf g steht und durch den Punkt (1/1) verläuft.
|
|
|
|
|
|
|
|
|
|
Letzte Änderung:
19.02.2009
© Pädagogisches Institut für die deutsche Sprachgruppe
- Bozen. 2000 -
|
|
|
|
 |
|
|
|
|