CAS-Werkzeug: Derive
Den Schnittpunkt zweier Geraden bestimmen

Abfolgeschritte

1. Eingabe der Geraden

Zwei Geraden mit den Funktionsvorschriften
f(x) und g(x)
sind eingegeben
und gezeichnet.

2. Geometrische Bestimmung des Schittpunktes mit dem Cursor

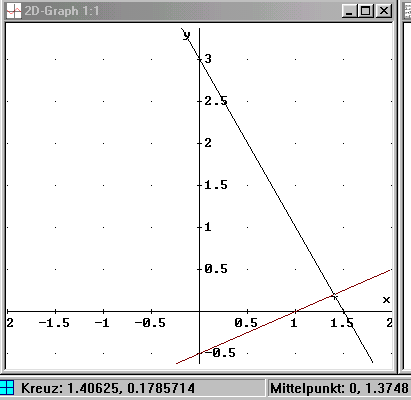
Mit den Symbolen "-> <-" für "Hinein Zoomen" wird im Grafikfenster die Eichung des Koordinatensystems vergrößert. Der Schnittpunkt wird exakter sichtbar.

Klickt man nun im Grafikfenster mit dem Cursor auf die Gerade f(x), so werden in der Statuszeile die Koordinaten des Punktes angezeigt. Im nebenstehenden Bild steht der Cursor nahezu auf dem Schnittpunkt. Er liege bei (1.40625 / 0.1785714) "sagt" die Statuszeile. Und: Vielleicht geht es mit guten Augen noch genauer!

3. Geometrische Bestimmung des Schittpunktes mit dem Spurmodus

In der nebenstehenden Abbildung sieht man in der Symbolleiste (oben) ein Symbol eingegraut. Es ist das Symbol für den Spur-Modus. Er ist aktiv.

Der Cursor verändert sich in ein kleines Quadrat. Er liegt jetzt bei Anklicken immer auf der aktiven Geraden. Durch mehrfaches Klicken auf der Geraden kann man sich mit dem Spurpunkt dem Schnittpunkt immer mehr nähern.

In nebenstehender Abbildung
steht der Spurpunkt auf den
Koordinaten (1/1).

4. Algebraische Bestimmung des Schnittpunktes:
die Bedingung für den Schnittpunkt eingeben

Das Algebrafenster wird aktiviert. Über die Eingabezeile gibt man für den Schnittpunkt die Bedingung #3: f(x) = g(x) ein, denn für den Schnittpunkt sind die Funktionswerte gleich.

Sodann vereinfacht man die Bedingung #3: mit dem
Symbol "=" (Vereinfachen).
Man erhält die Zeile #4.

5. Lösen der Gleichung:
die Koordinate für x finden

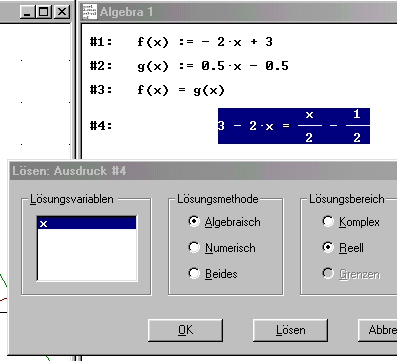
Die Lösung #6: für die Gleichung erhält man durch Anklicken des Symbols für "Ausdruck lösen" (Vergrößerungsglas).

Es öffnet sich das nebenstehende Fenster "Lösen: Ausdruck #4". Für die Lösungsvariable x
wird die Lösungsmethode "Algebraisch" und für
die Lösung "Reell" eingeben.

Klickt man nun auf OK oder auf "Lösen", so erhält man die
Lösung #6: für x.