|
Modellannahmen für
die Ausbreitungs- und Abklingphase eines grippalen
Infekts
Für die Ausbreitungsphase
wird angenommen:
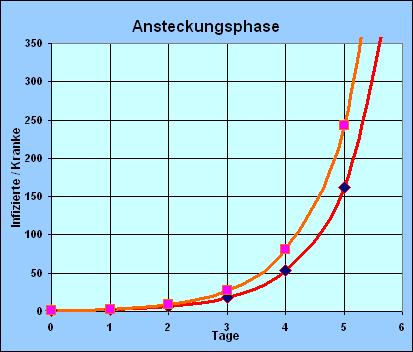
Die Inkubationszeit beträgt 0 Tage, die Ansteckungszahl
beträgt 2.
Für die Abklingphase
wird angenommen:
Die vor 7 Tagen infizierten Kinder sind
nach 7 Tagen (Heildauer) gesundet und können
niemanden mehr anstecken. Weiter wird angenommen,
dass die Schule insgesamt 384 Schüler hat.
|
|
|
Nach ...Tagen
|
Anste- ckungs-
zahl
|
Anzahl: "Neu-
infizierte"
|
Inkuba- tions-
zeit
|
|
Anzahl "Grippe-
kranke"
|
|
0
|
2
|
1
|
0
|
0
|
1
|
|
1
|
2
|
2
|
0
|
0
|
3
|
|
2
|
2
|
6
|
0
|
0
|
9
|
|
3
|
2
|
18
|
0
|
0
|
27
|
|
4
|
2
|
54
|
0
|
0
|
81
|
|
5
|
2
|
162
|
0
|
0
|
243
|
|
6
|
2
|
384 *)
|
0
|
0
|
384
|
|
7
|
2
|
0
|
0
|
1
|
383
|
|
8
|
2
|
0
|
0
|
2
|
381
|
|
9
|
2
|
0
|
0
|
6
|
375
|
|
10
|
2
|
0
|
0
|
18
|
|
|
|
2
|
0
|
0
|
|
|
|
|
2
|
|
0
|
|
|
|
|
Ideen für mögliche,
selbstorganisierte Übungen:
|
|
- Berechnet in der Tabelle oben jeweils die
Geheilten und Kranken. Vervollständigt
die Tabelle bis zu 14 Tagen Krankheitsausbreitung
und Abheilung.
- Experimentiert mit der folgenden Excel-Tabelle
und den folgenden Excel-Liniendiagrammen:
- Ändert in dem Modell zur Ausbreitung
und Abheilung einer grippalen Infektion die
Ansteckungszahl, die Inkubationszeit und Heildauer.
Erstellt dazu eigene Tabellen, ggf. mit Excel.
- Stellt eure eigenen Berechnungen für
die Infizierten, Geheilten und Kranken ebenfalls
in Liniendiagrammen dar.
- Warum muss auch bei diesen Modellierungen
von einem idealen Modell gesprochen werden?
|