So könnte die Anwendungsphase ablaufen:

1. UStd:
Einführende Diskussionen zum realen Problem in der Klasse; Entscheidung für die Bearbeitung einer Anforderung (Aufgabe) und Kleingruppenbildung

2. bis 4. UStd:
Mathematische Modellierungsarbeiten an der gewählten Aufgabe; sachangemessene Interpretation der mathematischen Ergebnisse; Erstellung einer Präsentation

5. und 6. UStd:
Präsentation der Kleingruppen-Ergebnisse in der Klasse und Diskussion aller Ergebnisse im Sachzusammenhang des realen Problems

1. Unterrichtsstunde

Einführende Diskussionen zum realen Problem in der Klasse

Entscheidung für die Bearbeitung einer Anforderung (Aufgabe) und Bildung von Kleingruppen

• durch eine mögliche Bild-Diskussion oder durch anregende Texte sowie
• durch einige "Blicke" auf das komplexe Klima-Problem.

1. Setzt euch auseinander mit den Analyse-Anforderungen für die Klassen 8 bis 10 auf der Seite Analysen: Energie u.a. aus fossilen Energieträgern und deren globale Klimafolgen und entscheidet euch für eine der möglichen Arbeiten.
2. Bildet auf der Grundlage eurer Entscheidung arbeitsteilige Kleingruppen und legt eine Arbeitsmappe an.

Die Seiten können ausgedruckt als "Arbeitsblätter" verwendet werden. Sie können, müssen aber nicht, auch am Computer eingesehen werden oder in der Klasse projiziert werden.
Die Eingangdiskussion sollte in jedem Fall stattfinden, damit die folgenden Modellierungsarbeiten durch die Jugendlichen in den gesellschaftlich bedeutungsvollen Sach-Zusammenhang des Klimawandels auf der Erde gebracht werden können.
Bei der Kleingruppenbildung sollte die Lehrperson beratend helfen.

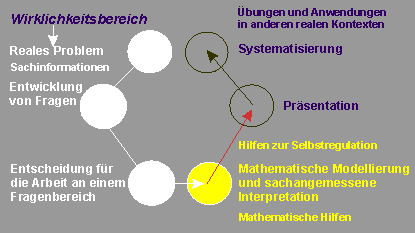
2. bis 4. Unterrichtsstunde

Mathematische Modellierungsarbeiten an der gewählten Aufgabe; sachangemessene Interpretation der mathematischen Ergebnisse; Erstellung einer Präsentation

Arbeitsaufträge

Die von der Lehrerin oder dem Lehrer beratenen Analyse- und Konstruktionsanforderungen führen zu den folgenden Arbeitsaufträgen:

1. Arbeitet in den nächsten drei Mathe-Stunden und auch Zuhause selbstreguliert (d.h. selbstständig, selbstorganisiert und selbstverantwortet) an den Aufgaben, für die ihr euch zuvor entschieden habt.
   Kleingruppe(n) 1:
   Analysen zur Energiegewinnung und zum "globalen" Energieumsatz
   Kleingruppe(n) 2:
   Analysen zum Ausstoß von Kohlendioxid und zur globalen Veränderung des Klimas
   Kleingruppe(n) 3:
   Analyse weiterer Zusammenhänge und Folgerungen daraus sowie Modellrechnungen a) zum Vorrat an fossilen Energieträgern und b) zur atomaren Risikoenergie
2. Ich werde euch bei eurer Arbeit beobachten (und ggf. bewerten, wie ihr euch in euren Kleingruppen gegenseitig helft und wie ihr miteinander kommuniziert und kooperiert). Wenn ihr aber nach einer eingehenden Beratung in eurer Kleingruppe mit eurer Arbeit nicht mehr weiter kommt, so berate ich euch auf Anfrage hin.
3. Stellt eure Arbeitsergebnisse in euren Arbeitsmappen dar. Nutzt dabei die euch bekannten Funktionen [(er)findet aber ggf. auch neue Mathe hinzu].
4. Interpretiert eure Ergebnisse im Kontext des global bedeutungsvollen Problems des Klimawandels auf der Erde.
5. Erstellt in eurer Kleingruppe eine Präsentation sowohl für die Arbeitsergebnisse als auch für die Interpretation. Hilfen findet ihr unter "Anregungen zur Präsentation der Arbeitsergebnisse" auf der Eingangsseite des realen Problems.

Wiederum kann die Seite (../ma0557.htm) ausgedruckt werden und bei der Aufgaben-Zuteilung genutzt werden. Die Seite kann auch nach Word exportiert und an die Situation der Klasse angepasst werden.
Sobald aber die Modellierungsarbeiten beginnen und Datenbestände etwa mit Excel ausgewertet werden oder selbstständig mit den mathematischen Hilfen gearbeitet werden soll, ist auch eine Arbeit am Computer notwendig.

Die Modellierungsarbeiten sollen in den Kleingruppen selbstreguliert (selbstorganisiert und selbstverantwortet) durchgeführt werden. Wichtig ist es, den Kontext zum Thema im Kopf zu behalten.

Die benannten Kleingruppen 1, 2 und 3 können mehrfach vorkommen. Es bietet sich auch Partnerarbeit an, wobei ein "kompetenter" Jugendlicher einen weniger kompetenten berät und fördert.

Die Lehrkraft coacht die Modellierungsarbeit. Sie sollte sich daher unbedingt alle anklickbaren Sachinformationen und alle mathematischen Hilfen zum realen Problem ansehen. Das ist wichtig, um den Kleingruppen, die irgendwo stecken bleiben, Tipps geben zu können. Sie sollte sich auch die ausgearbeitete mögliche Lösung zu Analysen zum Ausstoß von Kohlendioxid und zur globalen Veränderung des Klimas ansehen. Diese Lösung zeigt, was ggf. von den Kleingruppen erwartet werden kann oder sollte.

In dieser Anwendungsphase geht es auch darum, allgemein (prozessorientierte) mathematische Kompetenzen zu fördern. Sie können ebenfalls mit in die Bewertung der Jugendlichen eingeschlossen werden. Dann sollten die Jugendlichen dies aber vorher wissen. An dieser Stelle sei darauf verwiesen, dass prozessorientierte Kompetenzen nur in einem komplexeren Arbeits- oder Lern-Prozess angebahnt und gelernt werden können. Diese Kompetenzen lassen sich kaum didaktisch kleinschreiben.

Während der Vorbereitung des Unterrichts und auch in der Anwendungs-Modellierungsphase übernimmt die Mathematiklehrerin und der Mathematiklehrer in der Regel die Rolle eines kompetenten Laien.

Alle Schülerinnen und Schüler finden auf der Seite (../ma0557.htm) in der rechten Spalte anklickbare mathematische Hilfen.
Die Kleingruppen wenden lineare, quadratische und insbesondere Exponentialfunktionen an. Neu hinzukommende Mathematik etwa zu anderen Funktionen können zum Anlass genommen werden, sie nach der Präsentationsphase zu systematisieren.

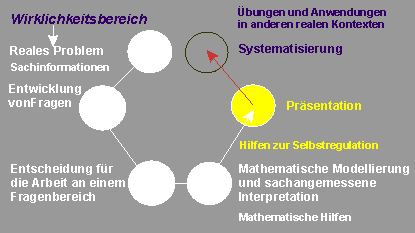
5. und 6. Unterrichtsstunde

Präsentation der Kleingruppen- Ergebnisse in der Klasse
und
Diskussion aller Ergebnisse
im Sachzusammenhang
des realen Problems

Arbeitsaufträge

Die Lehrerin oder der Lehrer stimmt sich mit den Kleingruppen ab, in welcher Reihenfolge die Präsentationen vor der Klasse erfolgen. Dann erteilt sie/er etwa die folgenden Arbeitsaufträge:

• Jede Kleingruppe stellt ihre Arbeitsergebnisse vor der Klasse so vor, dass alle anderen in der Klasse sie auch verstehen und nachvollziehen können. Also: Lasst immer genügend Zeit, damit die Anderen sich auch Notizen in ihrer Arbeitsmappe machen können. Hetzt nicht durch euren Vortrag.
• Hilfen findet ihr unter "Anregungen zur Präsentation der Arbeitsergebnisse"auf der Eingangsseite jedes realen Problems
• (Ggf.: Ich habe vor, die Präsentation zu bewerten.)
• Jede Kleingruppe beleuchtet in ihrem Vortrag das reale Problem unter einem anderen Gesichtspunkt. Alle diese hängen aber, wie wir in der Eingangsdiskussion des Problems bereits festgestellt haben, irgendwie miteinander zusammen. Und genau das wollen wir gemeinsam diskutieren, nachdem alle Vorträge gehalten sind. So wollen wir erreichen, dass es nicht bei der Summe (Addition) der Einzelbeiträge bleibt, sondern die Diskussion ein neues Ganzes erwirkt.
• In einem abschließenden fragend-entwickelnden Unterricht werden wir dann auch noch unter meiner Leitung die funktionale Modellierung präzisieren und ggf.mit der dynamischen Modellierung vergleichen.

Die Jugendlichen sollten durch die Gesamtheit der Präsentationen und abschließenden Diskussionen zur Erkenntnis gelangen, wie differenziert das globale Problem des Klimawandels ist und sie sollten sich auch mit möglichen Gegenmaßnahmen auseinandersetzen (emanzipatorische Kompetenzen!). Mathe bekommt so einen anderen Sinn als nur den, lediglich Selbstzweck zu sein.

Die Mathe-Lehrerin oder der Mathe-Lehrer nutzt die Präsentationen der Gruppen 1, 2 und 3 um die Nützlichkeit der Exponentialfunktion sowie anderer Funktionen zu verdeutlichen. Sie nutzt ggf. die Präsentationen einer Gruppe, die sich mit der Konstruktion und Simulation von dynamischen Wechselwirkungen zwischen Bevölkerung, Energiegewinnung und Kohlendioxidausstoß auseinander gesetzt hat dazu, die Begriffe der dynamischen Modellierung zu wiederholen und dazu, die funktionale mit der dynamischen Modellierung zu vergleichen.
Funktionale Modellierungen führen über Approximationen mit Funktionen zu möglichen Vorhersagen oder Prognosen für die nahe Zukunft. Dynamische Modellierungen führen zu Beschreibungen des Systemverhaltensvon zweckbedingt, untersuchten Modellen und erlauben Aussagen darüber, wie eine Veränderung der "Stellschrauben" (Parameter) im System der Informationsweitergabe wirkt.