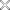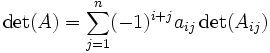| Detreminante mit Laplaceschem Entwicklungssatz Schreiben Sie ein Programm, welches die Determinante einer beliebigen m x m Matrix mit Hilfe des Laplaceschen Entwicklungssatzes mit Unterdeterminanten berechnet.
Bsp.:

Wenden Sie dabei das Prinzip „divide and conquer“, also „teile und herrsche“ an.
Die Determinante ist das Ergebnis einer speziellen mathematischen Funktion, die nur auf quadratische Matrizen anwendbar ist. Die Determinante gibt beispielsweise an, ob eine Matrix invertierbar ist oder ob ein Gleichungssystem, falls es als Matrix dargestellt wurde, lösbar ist.
Nähere Informationen zu Matrizen finden Sie hier (Wikipedia)
Links:
-Theorie zu Matrizen
-Weitere Aufgaben zu Matrizen:
allgemeine Operationen
Mathematische Operationen
Autor: J.B. - Gruppe 1
|