|
|
|
|
|
|
Im
Planetensystem der Erde lässt sich berechnen, zu welchen Zeiten wir
Sonnen- und Mondfinsternisse an bestimmten Orten auf der Erde beobachten
können. Wann eine Raumfähre an der Weltraumstation ankoppeln wird oder zu
welchen Zeitpunkten an welchen Orten wir Beobachtungs-Satteliten am Himmel
sehen können, das lässt sich im Gravitationssystem der Erde berechnen.
Und in Ökosystemen lässt sich das Wachstum der unterschiedlichen
Arten berechnen, die aufeinander einwirken.
Alle diese Systeme verändern sich in der Zeit. Sie sind dynamisch und
zeigen ein System-Verhalten, das innerhalb kleiner Fehlergrenzen
zeitlich vorhersagbar, also determiniert ist. |
| |
 |
|
 |
|
 |
| |
|
|
|
|
|
Ein
Planetensystem
|
|
Nordlichter
|
|
Eine
Schülerbande auf dem Schulhof
|
| |
Dynamische
Systeme - wie Nordlichter oder Schülerbanden auf einem Schulhof
- können auf kleinste Störungen so reagieren, dass ihr Verhalten
mitunter unvorhersagbar wird. Die Störungen können sich durch Kausalitäten
und Wechselwirkungen im System so aufschaukeln, dass in diesen Fällen
eine Vorhersage des Systemverhaltens unmöglich wird oder nur noch in
Wahrscheinlichkeiten ausgedrückt werden kann. Dynamische Systeme können
also ein stochastisches (zufälliges) Verhalten zeigen, dass nur noch
mit Wahrscheinlichkeiten vorhersagbar ist.
Viele stochastische Systeme sind aber in ihrem Verhalten genauer
vorhersagbar, als es bisher angenommen wurde. In früher gemessenen Daten,
die man als zu kompliziert beiseite geschoben hatte, können heute unter
Nutzung neuer mathematischer Verfahren und mit Hilfe von Computern
einfache Gesetze oder Ordnungen erkannt werden.
Mit dem stochastischen (man kann auch sagen: chaotischem) Verhalten von
Systemen, beschäftigt sich die Chaostheorie. So gesehen ist die Chaostheorie
also ein Spezialfall der Systemtheorie. |
| |
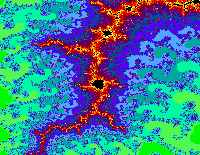
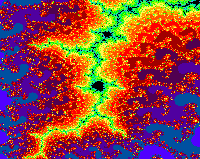
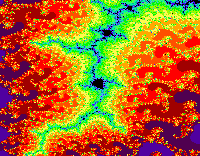
Drei
identische, lediglich farblich veränderte Bilder vom Rande der Mandelbrot-Menge
|
| |
Die
geometrische Sprache für das Verhalten von stochastischen (chaotischen)
Systemen ist u.a. die fraktale Geometrie. In ihrem unerschöpflichen
Vorrat an Formen lassen sich u.a. Galaxien, Wolkenbildungen, Blitze, Turbulenzen,
Mäanderungen und Eskalationen beschreiben. So wie Architekten auch noch
heute mit der traditionellen (u.a. euklidischen) Geometrie Häuser und Straßen
beschreiben können.
Chaosforschung richtet das Augenmerk auf versteckte Ordnungen sowie
auf "Empfindlichkeiten" und "Regeln" in Systemen. Chaosforschung erklärt,
wie sich Systeme selbst organisieren können und wie auf diese
Weise neue Qualitäten emergieren (sich entwickeln), die bis dahin
nicht existierten.
Die schrittmachenden
neuen Erkenntnisse durch die System- und Chaosforschung wurden mit
mathematischen Verfahren (u.a.mit der system-dynamics, der fraktalen
Geometrie, der fuzzy-logik sowie der Stochastik und Wahrscheinlichkeitslehre)
und mit Hilfe von schnellen Rechnern möglich.
Die Theorien
der Komplexität finden
Anwendung u.a. in der Makro- und Mikrophysik, der Ökologie, der
Evolutionstheorie, der Psychologie, der Soziologie, der Neuro- und Genforschung,
der "künstlichen Intelligenz" und der Wirtschaftstheorie.
Aber auch Kommunikation, Verständigung und Lernen lassen sich mit Hilfe
dieser Theorien modellieren.
|
| |
 |
|
 |
|
 |
| |
|
|
|
|
|
Mäanderungen
|
|
Eine
Galaxie
|
|
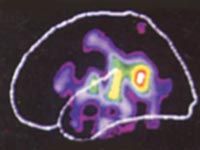
Gehirnaktivität
beim Hören eines Wortes
|
|
|
|