Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung;
bezogen auf die Klassen (9) 10 bis 12 |
| |
|
|
Hinweise:
Die Bearbeitung der folgenden Aufgaben kann Teil einer Gesamtlösung von mehreren arbeitsteilig arbeitenden Kleingruppen.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen wie im Fall der "Konstruktion von Wechselwirkungen zwischen Bevölkerung, Energie und CO2" |
|
Die folgenden Lösungen zur
können Teil einer Gesamtlösung sein, bei der weitere Kleingruppen parallel arbeiten an Konstruktionen und Simulationen dynamischer Wechselwirkungen zwischen Bevölkerung, Energieumsatz und Kohlendioxidausstoß.
Nach der Präsentation und Diskussion der Gruppenlösungen in der Klasse wird gemeinsam u.a. über den Sinn und Zweck dynamischer Modellierungen diskutiert.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 4 bis 5 Schulstunden notwendig, wenn auch Teilaufgaben zu Hause erledigt werden. Der Einsatz eines Werkzeugs z.B. Excel ist notwendig. Für eine Diskussion in der Klasse sind dann noch einmal 2 Schulstunden notwendig.
|
| |
|
|
|
|
|
|
|
Konstruktion und Simulation
von Wechselwirkungen
zwischen Bevölkerung, Energie und Kohlendioxid unter der Annahme zunehmender Enerneuerbarer Energien |
| |
|
|
In den Industrie-, Schwellen- und Entwicklungsländern gibt es ganz unterschiedliche Diskussionen zur Nachhaltigkeits-, Energie- und Klimapolitik sowie Szenarien zur Energieentwicklung und zu Klimaschutzzielen.
Konstruiert und simuliert auf diesem politischen Hintergrund unterschiedliche Szenarien für das "Klima":
|
|
Wortmodell zum Problem des Überhangs von Kohlendioxid in der Atmosphäre
Grüne Pflanzen sind in der Lage, Kohlendioxid aus der Luft und aus den Gewässern zu assimilieren und ihn in Kohlenhydrate umzubauen. Lichtenergie und Chlorophyll sind dabei notwendige Bedingungen. Werden fossile Energieträger verbrannt, so entsteht bei ausreichendem Sauerstoff wieder Kohlendioxid. Der Kreislauf des Kohlendioxids ist geschlossen. (Mehr dazu auf der Seite "Kohlenstoff, der natürliche Kreislauf von Kohlendioxid und die "Klimaglocke Erde").
Wird in kleineren Zeiträumen mehr Biomasse verbrannt, als durch Photosynthese in dieser Zeit entstanden ist, so gibt es in der Atmosphäre einen Überhang an ausgestoßenem Kohlendioxid. Dieser Überhang lag vor der Industrialisierung noch bei etwa 280 ppm. Er stieg bis heute auf 381 ppm an. Und durch Verbrennen von fossilen Brennstoffen in Wärmekraftwerken werden jährlich ca. 32 Mrd. Tonnen CO2 emittiert, von denen etwa die Hälfte in der Atmosphäre verbleibt.
Der Kohlenstofffluss in die Atmosphäre beträgt zur Zeit 6 Gt pro Jahr; er wächst weiter um etwa 1,5 % jährlich. Doch die Ozeane entziehen der Atmosphäre schätzungsweise 5,5 bis 9,5 Mrd. Tonnen CO2. Dort wird es auch zum Teil wieder gelagert. (Quelle der Zahlen: BINE bildungsinfo 3.)
Einstiegsmodell zu Wechselwirkungen zwischen Bevölkerung, Energieumwandlung und Kohlendioxid in der Atmosphäre
Dieses Einstiegsmodell wird unter der Annahme konstruiert, dass schließlich nur noch Erneuerbare_Energien zur Energiegewinnung genutzt werden.
Das auf der Seite zuvor dargestellte Wirkungsdiagramm bleibt im Wesentlichen erhalten, wird aber ergänzt. Jetzt wird angenommen, dass die Erneuerbaren_Energien rückgekoppelt zum Wachsen der gesellschaftlich geforderten Gesamtenergie zunehmen und die Fossilen_Energien ersetzen. Je mehr erneuerbare Energien verfügbar sind, desto weniger fossile Energien müssen noch umgewandelt werden. Und nur die verbleibenden fossilen Energien wirken dann noch positiv auf ein Anwachsen des Kohlendioxids in der Atmosphäre. Ein mögliches Wirkungsdiagramm kann wie folgt aussehen. |
| |
|
|
| Nehmt z.B. für die nächsten 50 Jahre kleiner werdende Anteile von fossiler Energie gegenüber erneuerbaren Energien an. |
|
 |
| |
|
|
Diskutiert in eurer Kleingruppe mögliche Zustandsgrößen, Flussgrößen, Parameter und Konstante in diesem Modell.
|
|
Bei der Übertragung des Wirkungsdiagramms in ein Flussdiagramm wird überlegt, welche Flussgrößen und Faktoren zusätzlich zu dem zuvor behandelten Modell abstrahiert werden können.
Auf die „Gesamt_Energie“ (E) wirkt jetzt gewissermaßen als „Sterbezahl“ die Flussgröße „Zunahme_Erneuerbare_Energien“ (ZEE) mit einem Faktor (feE). ZEE quantifiziert - qua Rückkopplung - den wachsenden Anteil an erneuerbare Energien, der von der Gesamtenergie (E) subtrahiert wird. Als Gesamtenergie bleiben dann gewissermaßen nur die abnehmenden fossilen Energien übrig, weil in diesem Modell nur zwischen erneuerbaren und fossilen Energien unterschieden wird.
|
| |
|
|
| Stellt das Modell in Form eines Flussdiagramms dar. |
|

|
| |
|
|
| Beschreibt die Wechselwirkungen (bzw. die direkten Abhängigkeiten) in Zustands- und Modellgleichungen. |
|
Die folgenden Zustands- und Modellgleichungen lassen sich aus dem Flussdiagramm erschließen. Das Modell wird quantifiziert indem alle Größen mit Zahlen belegt werden.
B_neu <-- B_alt + Δt · Zb;
Anfangsgröße B = 7 Milliarden; Δt = 1 (Zeittakt 1 Jahr)
E_neu <-- E_alt + Δt · (Ze - ZEE);
Anfangsgröße E = 18 GWh; Δt = 1 (Zeittakt 1 Jahr)
C_neu <-- C_alt + Δt · Zc;
Anfangsgröße C =3,81 · 10² ppm; Δt = 1 (Zeittakt 1 Jahr)
Zb = r · B; r = 0,01 (daher Zeittakt 1 Jahr)
Ze = fe · B; fe = 0,01
ZEE = feE · E; feE= 0,1
Zc = fc · E; fc = 0,005
Zur Bestimmung der Anfangsgrößen und der Wachstumsziffer der Erdbevölkerung sowie zur Abschätzung der Binde-Faktoren wird auf die folgenden Sachinformationen verwiesen (Wachstum der Weltbevölkerung, Energie-"Verbrauch" , Energiegewinnung aus fossilen Energieträgern sowie Ausstoß von Kohlendioxid). Aber die beiden Binde-Faktoren fe und fc hängen auch vom Zweck des Modells ab: einer Grundeinsicht oder Grunderkenntnis. Wobei feE als fiktive Größe so bestimmt ist, dass nach etwa 30 Jahren fast keine fossilen Energien mehr umgewandelt werden. |
| |
|
|
Programmiert die Zustands- und Modellgleichungen und simuliert das konstruierte Modell.
|
|
Die programmierte - und damit simulierbare - Tabelle und auch ein Simulationsergebnis siehe:
ExcelDateien/Mappe1558e.htm (nur zur Ansicht) oder ExcelDateien/Mappe1558e.xls (herunterladbar und interaktiv) |
| |
|
|
Hier ein mögliches Simulationsergebnis, das zur Tabelle passt
blau = Kohlendioxid;
rot = Energie;
gelb = Bevölkerung
|
|
 |
| |
|
|
| Beschreibt das Verhalten dieses einfachen Modells, interpretiert es und beschreibt den Zweck und die Grenzen dieses Modells. |
|
Der Kohlendioxidgehalt in der Atmosphäre wächst zunächst weiter und nähert sich einem hohen Grenzwert, selbst dann wenn sich „die Staaten der Welt in vorbildlicher Manier einigten, ihre Emissionen auf den Stand von 1990 oder früher zurückzufahren. ... Der CO2-Gehalt in der Luft würde damit aber noch nicht gesenkt ... Die Temperatur folgt wiederum der Konzentration mit einer gehörigen Verzögerung, die Jahrzehnte beträgt. Jene Erwärmung, die wir heute beobachten, ist nicht das Ergebnis heutiger Emissionen, sondern ein Erbe der Vergangenheit. ....
Und die Erwärmung der Erde geht weiter, global durchschnittlich um 1,8 bis 4 Grad Celsius bis zum Jahr 2100. Diese Erwärmung lässt sich wahrscheinlich nicht aufhalten, wohl aber verlangsamen: Dazu muss u.a. der Ausstoß an Kohlendioxid in den nächsten 150 Jahren auf 25 % des heutigen Standes reduziert werden." (Quelle: DIE ZEIT, vom 4.3.2010).
|
|
|
|
|
|
Konstruktion und Simulation von Wechselwirkungen
zwischen Bevölkerung, Energieumsatz und
"Abbau" von Kohlendioxid aus der Atmosphäre |
| |
|
|
In den Industrie-, Schwellen- und Entwicklungsländern gibt es ganz unterschiedliche Diskussionen zur Nachhaltigkeits-, Energie- und Klimapolitik sowie Szenarien zur Energieentwicklung und zu Klimaschutzzielen.
Nehmt z.B. an, dass die Bevölkerung mit zunehmender Bildung dafür sorgt, dass z.B. immer wieder Wälder aufgeforstet und neu angelegt werden. |
|
Wortmodell zur Vision eines klimafreundlichen, menschlichen Handelns
Dazu werden zur Zeit zwei Szenarien diskutiert:
- Abbau von CO2 durch Bindung von CO2 u.a. durch künstlich erzeugte Algenblüten in den Weltmeeren oder
- Abbau von CO2 durch Erhöhung der Photosynthese in „grünen Pflanzen“ auf dem Land, also etwa durch Wiederaufforstung und Anbau von Wäldern.
Beide Szenarien entsprechen dem Wunsch, sich dem natürlichen Kreislauf von Kohlendioxid wieder anzunähern.
"Trotz der hohen Unsicherheiten und des Widerstandes von einigen Vertragsstaaten wurde auf der Klimakonferenz in Bonn im Jahre 2009 beschlossen, Senkenprojekte (u.a. grüne Wälder) für Kohlendioxid bei der Erfüllung der Verpflichtungen einzubeziehen" (Wikipedia).
Ein mögliches Wirkungsdiagramm:
Das obige Wirkungsdiagramm wird ergänzt. Die Fossilen_Energien werden zunehmend durch Erneuerbare_Energien ersetzen und es werden alle abgeholzten Wälder wieder aufgeforstet und neue Wälder gepflanzt.
Das Waldwachstum wirkt auf sich selbst. Es ist rückgekoppelt. Denn je mehr Wälder die Menschen in Funktion sehen, umso stärker wird ihr Wunsch, mehr Wälder anzupflanzen. Und: Je mehr Wälder dann im natürlichen Kreislauf des Kohlendioxids vorhanden sind, um so mehr Kohlendioxid wird abgebaut. Ein mögliches Wirkungsdiagramm kann wie folgt aussehen. |
| |
|
|
| Stellt die Wechselwirkungen in einem Wirkungsdiagramm dar.
|
|
 |
| |
|
|
| Diskutiert sodann in eurer Kleingruppe mögliche Zustandsgrößen, Flussgrößen, Parameter und Konstante in diesem Modell. |
|
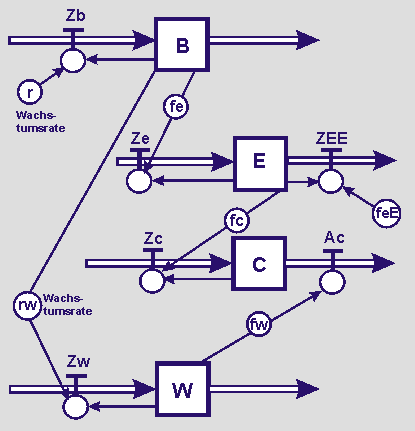
Zum obigen Flussdiagramm kommt im folgenden möglichen Flussdiagramm nun eine weitere Zustandsgröße W (Wälder) hinzu. Das ist die Annahme im vorstehenden Wirkungsdiagramm. Auf W wirkt eine Flussgröße Zw, die auf der Grundlage zunehmender Bildung in der wachsenden Welt-Bevölkerung beruht und von einem Wachstumsfaktor rw abhängig ist. Das zunehmende "Grün" der Wälder wirkt über einen Faktor fw abnehmend auf das bisher in die Atmosphäre eingebrachte Kohlendioxid.
|
| |
|
|
| Zeichnet ein Flussdiagramm und beschreibt die Wechselwirkungen in Zustands- und Modellgleichungen. |
|
 |
| |
|
|
| Beschreibt die Wechselwirkungen in Zustands- und Modellgleichungen.
|
|
Die folgenden Zustands- und Modellgleichungen lassen sich aus dem Flussdiagramm erschließen. Das Modell wird quantifiziert indem alle Größen mit Zahlen belegt werden.
B_neu <-- B_alt + Δt · Zb;
Anfangsgröße B = 7 Milliarden;
E_neu <-- E_alt + Δt · (Ze - ZEE);
Anfangsgröße E = 18 GWh;
C_neu <-- C_alt + Δt · (Zc - Ac);
Anfangsgröße C =3,81 · 10² ppm;
W_neu <-- W_alt + Δt · Zw
Anfangsgröße W = 40 Millionen km2.
Δt = 1 (Zeittakt 1 Jahr)
Zb = r · B; r = 0,01 (daher Zeittakt 1 Jahr)
Ze = fe · B; fe = 0,01
ZEE = feE · E; feE= 0,1
Zc = fc · E; fc = 0,005
Ac = fw · W; fw = 0,001
Zw = rw · B; rw = 0,01
Zur Bestimmung der Anfangsgrößen von B, E und C sowie der Wachstumsziffer der Erdbevölkerung und zur Abschätzung der Binde-Faktoren gilt das oben Gesagte.
Als Maßgröße für W nehmen wir die heutige weltweite Waldfläche von 40 Millionen km2 (Wikipedia, Wald). Die Wachstumsrate rw für Wälder und der Faktor fw sind aber fiktiv daran orientiert, dass die Menschheit in der Lage ist, sich selbst zu retten und klimafreundlich und humanverträglich zu handeln. |
| |
|
|
| Programmiert die Zustands- und Modellgleichungen und simuliert das konstruierte Modell. |
|
Die programmierte Tabelle für den Fall A und auch ein Simulationsergebnis siehe:
ExcelDateien/Mappe1558f.htm (nur zur Ansicht) oder ExcelDateien/Mappe1558f.xls (herunterladbar und interaktiv)
|
| |
|
|
Hier ein mögliches Simulationsergebnis, das zur Tabelle passt
grün = Wälder
blau = Kohlendioxid;
rot = Energie;
gelb = Bevölkerung
|
|
 |
| |
|
|
| Beschreibt das Verhalten des Modells, interpretiert es und beschreibt den Zweck und die Grenzen dieses Modells. |
|
Zum Bevölkerungswachstum und zum Wachstum der Energieumwandlung siehe die Beschreibung zum vorhergehenden Modell.
In diesem visionären Modell steigt die Fläche der Wälder im Zeitraum von 50 Jahren von 40 Millionen km² auf rund 44,5 Millionen km². (Zum Vergleich: Deutschland hat eine Landfläche von 349.223 km² ≈ 0,35 Millionen km² ). Würden also in den nächsten 50 Jahren alle 10 Jahre 0,9 Millionen km² Wald auf der Erde hinzukommen, so würde bei den obigen Annahmen und einer einsichtsfähig handelnden Gesellschaft der Kohlendioxidgehalt in der Atmosphäre von rund 380 ppm wieder auf rund 280 ppm sinken können. Und das wäre der CO2 Gehalt in der Atmosphäre vor der Industrialisierung, also der natürliche Kreislauf von CO2.
Die Grenze dieses Modell zeigt sich aber darin, dass das hier angenommene Wachstum von Wäldern unrealistisch ist, weshalb es höchstens als Konstante (also ohne Rückkopplung) oder rw als Zeitfunktion angenommen werden sollte. Dann aber sind weitere CO2 abbauende Maßnahmen in das Modell einzubauen, wenn die klimafreundliche Vision modelliert werden soll. Diese weiteren möglichen Modellierungen unterbleiben hier, sie können aber selbstständig durchgeführt werden.
Der Zweck dieses Modells ist aber auch schon damit erreicht, dass erkannt werden kann, dass die Menschheit in der Lage wäre, ihre selbstverschuldete Klimaverschlechterung mindestens zu bremsen.
|
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |


















