Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung;
bezogen auf die Klassen (8) 9 bis 12 |
| |
|
|
Hinweis:
Die Bearbeitung der Aufgaben zur "Konstruktion und Simulation von dynamischen Wechselwirkungen bei der Ausbreitung von Epidemien und insbesondere von AIDS" kann Teil einer Gesamtlösung von arbeitsteilig arbeitenden Kleingruppen sein.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben |
|
Die folgenden Lösungen zur Konstruktion und Simulation eines
können Teil einer Gesamtlösung sein (bei der ggf eine weitere Kleingruppe parallel an einer Analyse der Ausbreitung des HI-Virus, der diagnostizierten AIDS-Fälle und der an AIDS gestorbenen Deutschen
arbeitet).
Nach der Präsentation und Diskussion der Gruppenlösungen in der Klasse wird gemeinsam auch über den Sinn und Zweck dynamischer Modellierungen diskutiert.
Für die Erarbeitung der nachfolgenden Lösungen und deren Formulierung sind etwa 4 bis 5 Schulstunden notwendig, wenn auch Teilaufgaben zu Hause erledigt werden. Der Einsatz eines Werkzeugs z.B. Excel ist notwendig. Für eine Diskussion in der Klasse sind dann noch einmal 2 Schulstunden notwendig. |
| |
|
|
| |
|
|
| |
|
|
|
|
|
|
|
Konstruktion und Simulation
eines einfachen
dynamischen Modells
zur Ausbreitung einer Infektion |
| |
|
|
Konstruiert ein einfaches dynamisches Modell für die Ausbreitung einer Infektion.
|
|
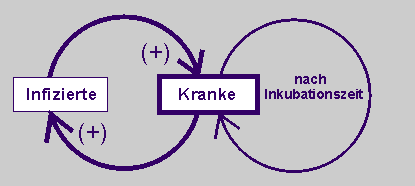
Bereits Infizierte werden nach einer gewissen Zeit (Inkubationszeit) krank und stecken dann immer wieder noch nicht Infizierte an. Die Zahl der Kranken wirkt positiv auf die Zahl der Infizierten: Je mehr Kranke es gibt, desto mehr Menschen können infiziert werden, desto mehr Infizierte wird es geben.
Das folgende Wirkungsdiagramm beschreibt die Abhängigkeiten in qualitativer Form. Es wird mit dem Pluszeichen oder mit „je desto“ argumentiert.
|
| |
|
|
| Beschreibt die Ausbreitung der Infektion zunächst in einem Wirkungsdiagramm. |
|
 |
|
|
|
| Diskutiert miteinander, welche wichtige Zustands- und Flussgröße und welchen Parameter ihr berücksichtigen müsst. |
|
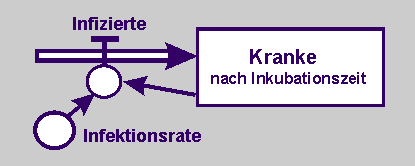
Wir übertragen das Wirkungsdiagramm in ein Flussdiagramm und quantifizieren auf diese Weise den Zusammenhang. Die Zustandsgröße Kranke (K) ist leicht zu erkennen. Flussgröße sind die immer wieder neu Infizierten (I). Auf sie wirkt eine Infektionsrate (r) und die Zahl der bereits Kranken.
Die Infizierten werden erst nach einer Inkubationszeit krank. Diese bleibt hier unbeachtet. Siehe gegebenenfalls aber "Ideale Modelle zur Ansteckungs- und Abklingphase eines Infekts" in der Lernumgebung "Mathe Überall". |
| |
|
|
| Beschreibt euer Modell sodann in einem Flussdiagramm. |
|
 |
|
|
|
| Beschreibt euer Modell durch eine Zustands- und eine weitere Modellgleichung. |
|
Die Zustands- und Modellgleichung lassen sich aus dem Flussdiagramm unter Berücksichtigung eines Zeittaktes erschließen. Alle Größen werden mit Zahlen belegt. Das Modell ist nun vollends quantifiziert.
K_neu <-- K_alt + Δt · I;
Anfangsgröße: K = 3; Δt = 1; (Interpretation 1 Tag
I = K · r;
Infektionsrate: r = 0,1 (oder Ansteckungsrate) |
| |
|
|
| Programmiert euer Modell in einer Excel-Tabelle auf der Grundlage der Zustands- und Modellgleichung. |
|
Siehe hierzu:
ExcelDateien/Mappe1628a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1628a.xls (herunterladbar und interaktiv)
Anmerkung: Zur Programmierung siehe: Crash-Kurse: Einführung in die Nutzung von Excel |
|
|
|
| Simuliert euer Modell und überlegt, wie ihr die Infektionsrate in der Schule bestimmen könnt. |
|
Das folgende Simulationsergebnis passt zu den Werten der Tabelle. In dieser Tabelle lassen sich aber die Anfangsgröße und die Infektionsrate verändern. Geschieht dies, so ergibt sich ein anderes Simulationsergebnis.
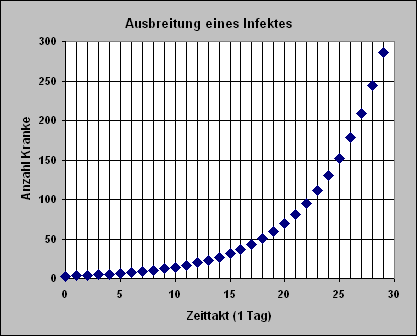
In einer Schule könnte durch Abzählen der Kranken zu Beginn und am Ende einer Woche simulativ die Ansteckungsrate bestimmt werden.
Im Fall einer sehr ansteckenden Infektion gibt es eine Meldepflicht bei der Gesundheitsbehörde. Auch die Behörde kann auf der Grundlage der Meldungen die Infektionsrate berechnen. |
|
|
|
| Beschreibt das Systemverhalten, den Zweck und die Grenzen des betrachteten Modells. |
|
Erhöhen wir die Infektionsrate, so ergibt sich bei gleich bleibender Anfangsgröße schnell ein völlig anderes Bild. Erst recht steigt die Zahl der Kranken rasend schnell, wenn auch noch die Anfangsgröße erhöht wird. Eine Infektion breitet sich exponentiell aus (siehe hierzu die zweite Grafik unter ExcelDateien/Mappe1628a.htm).
Die Simulationen verdeutlichen aber, dass hoch ansteckende Infektionen meldepflichtig sind. Diese Erkenntnis vermittelt das einfache Modell. Denn die Gesundheitsbehörde kann dann ggf. einen Kindergarten oder auch eine Schule für die Zeit der hohen Ansteckungsgefahr schließen.
Das Modell ist aber zur Beschreibung einer Epidemie nicht unbedingt geeignet. Denn es beschreibt lediglich die Ausbreitung der Infektion. |
|
|
|
|
|
Konstruktion und Simulation eines dynamischen Modells
zur Ausbreitung einer Epidemie oder Pandemie |
| |
|
|
| Konstruiert ein dynamisches Modell für die Ausbreitung einer Epidemie oder Pandemie.
|
|
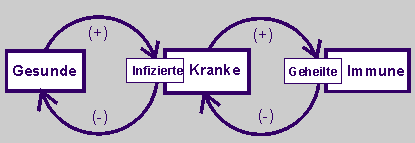
Wir modellieren nunmehr den Fall einer Epidemie und betrachten, wie sich die Anzahl von Gesunden, Kranken und schließlich Immunen ändert. Gesunde werden infiziert und dann krank. Kranke erholen sich, werden geheilt und sind dann für eine Zeit immun gegenüber der infektiösen Krankheit. Diese Wirkungen sind positiv.
Aber je mehr Kranke es gibt, desto weniger Gesunde wird es geben. Die Anzahl der Kranken wirkt negativ auf die Anzahl der Gesunden. Entsprechend wirkt die Anzahl der Immunen auf die Anzahl der Kranken.
Das folgende Wirkungsdiagramm beschreibt die Zusammenhänge qualitativ. Es wird gefragt, Was wirkt auf Was und wie. Argumentiert wird mit dem Plus- oder Minuszeichen oder mit „je desto“. |
| |
|
|
| Beschreibt die Ausbreitung der Infektion zunächst in einem Wirkungsdiagramm. |
|
 |
|
|
|
| Diskutiert, welche Zustandsgrößen, Flussgrößen und Parameter ihr berücksichtigen müsst. |
|
Bei einer Quantifizierung des Wirkungsdiagramms in das folgende Flussdiagramm sind die Gesunden (Ges), Kranken (Kra) und Immunen (Imm) die Zustandsgrößen. Sie sind quasi hintereinander geschaltet. Die Zahlen folgen auseinander.
Die Zahl der Infizierten (In) und die der immer wieder Geheilten (Ge) sind die Flussgrößen. Auf die Flussgröße der Infizierten wirken die Infektionsrate (ir) und der Zahl der Gesunden. Entsprechend wirken auf die Zahl der Geheilten die Heilungsrate (hr) und der Zahl der Kranken.
|
| |
|
|
| Und beschreibt sodann euer Modell in der Flussdiagramm-Symbolik |
|
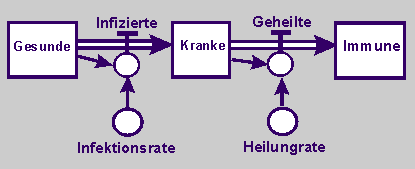 |
|
|
|
| Beschreibt sodann das Modell durch Zustands- und weitere Modellgleichungen.
|
|
Die Zustands- und Modellgleichungen lassen sich aus dem Flussdiagramm erschließen unter Berücksichtigung eines Zeittaktes zwischen Zustand_alt und Zustand_neu erschließen. In diesen Gleichungen wird das Modell einen weiteren Schritt quantifiziert. Alle Größen werden mit Zahlen belegt.
Ges_neu <-- Ges_alt + Δt · (-In);
Anfangsgröße: Ges = 5000; Δt = 1; (Zeittakt: 1 Tag oder 1 Woche ...)
Kra_neu <-- Kra_alt + Δt · (In - Ge);
Anfangsgröße: Kra = 0 ; Δt = 1; (Zeittakt: 1 Tag oder 1 Woche...)
Imm_neu <-- Imm_alt + Δt · (Ge);
Anfangsgröße: Imm = 0; Δt = 1; (Zeittakt: 1 Tag oder 1 Woche...)
In = Ges · ir; Infektionsrate: ir = 0,1;
Ge = Kra · hr; Heilungsrate: hr = 0,035
Woher die Werte für die Raten kommen, das siehe oben und auch unter Sach-Informationen zu Grippen, SARS und andere viröse Krankheiten). Im vorstehenden Modell werden die Infektions- und Heilungsrate als nahezu gleich angenommen. Die Heilungsrate „hinkt“ im obigen Modell aber etwas hinter der Infektionsrate her.
Allgemein gilt, dass die Infektions- und Heilungsrate vom Typ der Epidemie abhängen aber auch voneinander abhängen können. Es ist z.B. ein Unterschied, ob sich eine normale Grippe oder AIDS oder SARS ausbreitet. |
| |
|
|
| Programmiert das Modell in einer Excel-Tabelle. |
|
Die Zustands- und Modellgleichungen lassen sich in einer Excel-Tabelle programmieren. Zwar können die Werte immer noch selbstständig berechnet werden, aber es wird zunehmend zeitaufwändiger, insbesondere dann, wenn bei jeder Simulation alle Werte der Tabelle neu berechnet werden müssen.
Siehe hierzu:
ExcelDateien/Mappe1628b.htm (nur zur Ansicht) oder ExcelDateien/Mappe1628b.xls (herunterladbar und interaktiv)
Die Zahl der Infizierten und Geheilten ist jeweils auf null Stellen hinter dem Komma gerundet. Mathematisch ist das ein Fehler, interpretativ gibt es aber nur ganze Menschen! |
|
|
|
| Simuliert das Modell zur Ausbreitung einer Epidemie oder Pandemie. |
|
Das folgende Simulationsergebnis passt zu den Werten der Tabelle. In der Tabelle lassen sich die Anfangsgrößen und Raten sowie Delta t ändern. Geschieht dies, so ergibt sich jeweils ein anderes (ggf. auch nicht mehr interpretierbares) Simulationsergebnis.
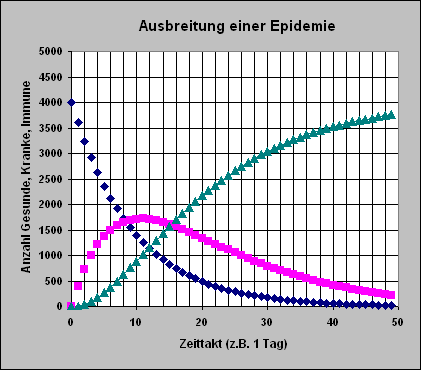
|
|
|
|
| Beschreibt sodann das Systemverhalten, den Zweck und die Grenzen des betrachteten Modells. |
|
In den ersten 30 Tagen werden in diesem simulierten Fall nicht alle Erkrankten (violett) geheilt und dann immun (grün). Was geschieht aber nach 50 oder 60 oder 70 Tagen bei niedriger Infektionsrate und höherer Heilungsrate? Oder was geschieht, wenn die Anfangswerte geändert werden?
In diesem dynamischen Modell der Ausbreitung einer Epidemie nimmt die Zahl der Gesunden in der ersten Zeit schnell ab und nähert sich dann langsam nahezu der Null. Alle werden krank. Die Zahl der Kranken steigt schnell auf einen Höchstwert, nicht ganz halb so groß, wie der Anfangswert der Gesunden. Dann sinkt die Zahl der Kranken - langsamer werdend - auch gegen Null ab. Die Zahl der Immunen steigt zunächst schnell an und strebt dann langsamer werdend einem Höchstwert zu, der dem Anfangswert der Gesunden entspricht. Schließlich sind alle Kranken immun geworden, also wieder gesund.
Wird Delta t verkleinert, so zieht sich der beschriebene Prozess über eine längere Zeit hin. Der gesamte Zeitablauf wird verzögert.
Die Modellierung endet also - nach einer quantitativen Phase - mit einer Verhaltensbeschreibung, die wieder qualitativ ist. Das ist in diesem Fall aber der Zweck des Modells. Es vermittelt die grundlegende (qualitative) Einsicht : So läuft generell eine Epidemie ab! Sollen quantitative Prognosen erstellt werden, müssen die Infektions- und Heilungsrate zum Typ der Epidemie passen.
Aber in diesem Modell erkranken alle Gesunden und werden schließlich immun. Das muss aber so nicht sein. Es gibt z.B. auch Ausbreitungen von Viren, die zum Tod führen. Hier liegt also eine Grenze des Modells. |
|
|
|
|
|
Konstruktion und Simulation eines dynamischen Modells
zur Ausbreitung von Viren mit Todesfällen |
| |
|
|
| Konstruiert ein dynamisches Modell zur Ausbreitung von Viren mit Todesfällen. |
|
Wir modellieren nun die Ausbreitung eines Virus, der alle Menschen infizieren kann und der nach Heilung zur Immunität oder auch zum Tod führen kann.
Gesunde werden z.B. mit Viren infiziert und dann krank. Sie haben z.B. eine Vogelgrippe oder AIDS. Eine Zahl von Kranken stirbt, andere werden ggf. geheilt und dann immun.
Die zunehmende Zahl von Kranken wirkt negativ auf die Zahl der Gesunden zurück. Je mehr Menschen mit einem Virus infiziert werden, desto weniger sind gesund. Und sowohl die Zahl der Immunen als auch die Zahl der Verstorbenen wirkt negativ auf die Zahl der Kranken zurück. Je mehr Menschen immun werden oder sterben, desto weniger sind krank.
Bei der Gestaltung des folgenden Wirkungsdiagramms wird gefragt: Was wirkt auf Was und wie? Argumentiert wird mit dem Pluszeichen oder mit „je desto“. Das Wirkungsdiagramm beschreibt die Zusammenhänge qualitativ. |
| |
|
|
| Beschreibt die Ausbreitung der Viren mit Todesfällen zunächst in einem Wirkungsdiagramm. |
|
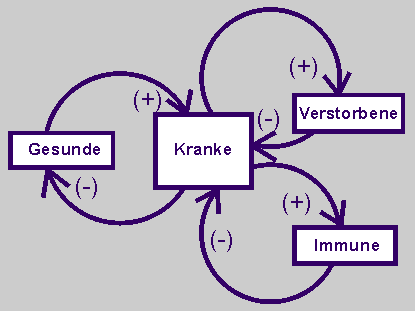 |
| |
|
|
| Diskutiert, welche Zustandsgrößen, Flussgrößen und Parameter ihr berücksichtigen müsst. |
|
Bei der Übertragung des qualitativen Wirkungsdiagramms in das folgende quantifizierte Flussdiagramm sind die Gesunden (Ges), Kranken (Kra), Verstorbenen (Ver) und Immunen (Imm) die Zustandsgrößen.
Die Zahl der Infizierten (In) ergibt sich aus der Zahl der Gesunden über die Infektionsrate (ir). Aus der Zahl der Kranken ergibt sich über die Sterberate (sr) die Zahl der Todesfälle (To) und über die Heilungsrate (hr)die Zahl der Immunen (Imm). |
| |
|
|
| Beschreibt sodann euer Modell in der Flussdiagrammsymbolik. |
|
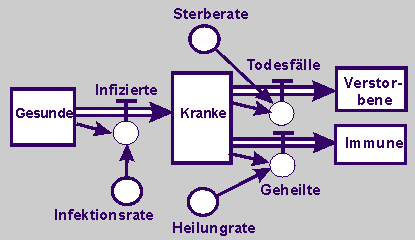 |
| |
|
|
| Beschreibt euer Modell durch Zustands- und Modellgleichungen. |
|
Die folgenden Zustands- und Modellgleichungen quantifizieren das Modell einen weiteren Schritt. Sie lassen sich aus dem Flussdiagramm unter Berücksichtigung eines Zeittaktes zwischen Zustand_alt und Zustand_neu erschließen. Alle Größen werden mit Zahlen belegt.
Ges_neu <-- Ges_alt + Δt · (-In);
Anfangsgröße: Ges = 5000;
Δt = 1 (Interpretation: Zeittakt 1 Tag, 1 Monat, 1 Jahr ....)
Kra_neu <-- Kra_alt + Δt · (In - (Ge + To));
Anfangsgröße: Kra = 0;
Imm_neu <-- Imm_alt + Δt · (Ge);
Anfangsgröße: Imm = 0;
Ver_neu <-- Ver_alt + Δt · (To);
Anfangsgröße: Ver = 0;
In = Ges · ir Infektionsrate: ir = 0,1;
Ge = Kra · hr Heilungsrate: hr = 0,08;
To = Kra · sr Sterberate: sr = 0,01
Woher die Werte für die Raten kommen, das siehe unter Sach-Informationen zu Grippen, SARS und andere viröse Krankheiten). Im vorstehenden Modell werden die Infektions- und Heilungsrate als nahezu gleich angenommen. Die Heilungsrate „hinkt“ im obigen Modell aber etwas hinter der Infektionsrate her. Die Sterberate ist gering gehalten, sie „hinkt“ damit erheblich hinter der Heilungsrate her.
Allgemein hängen die Raten vom Virus-Typ ab. Es ist z.B. ein Unterschied, ob sich eine normale Grippe oder AIDS ausbreitet. |
| |
|
|
| Programmiert das Modell in einer Excel-Tabelle auf der Grundlage von Zustands- und Modellgleichungen. |
|
Die Zustands- und Modellgleichungen lassen sich in einer Excel-Tabelle programmieren. Die selbstständige Berechnung der Werte ist nunmehr kaum noch möglich.
Siehe hierzu:
ExcelDateien/Mappe1628c.htm (nur zur Ansicht) oder ExcelDateien/Mappe1628c.xls (herunterladbar und interaktiv)
Die Zahl der Infizierten und Geheilten ist jeweils auf null Stellen hinter dem Komma gerundet. Mathematisch ist das ein Fehler, interpretativ gibt es aber nur ganze Menschen! |
|
|
|
| Simuliert das Modell zur Ausbreitung von Viren mit Todesfällen.
|
|
Das dargestellte Simulationsergebnis passt zu den Werten der vorstehenden Excel-Tabelle. Der Zeittakt muss interpretiert werden.
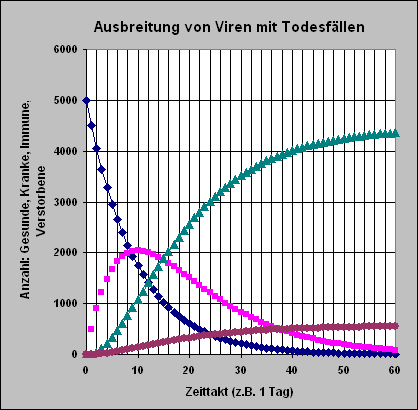
(blaue Raute = Gesunde; violettes Quadrat = Kranke;
grünes Dreieck = Immune und roter Punkt = Todesfälle)
In der Tabelle lassen sich alle stärker unterlegten Werte ändern. Geschieht dies, so ergibt sich jeweils ein anderes Simulationsergebnis. Bei einem weiteren Simulationsergebnis sind, bei Beibehaltung aller anderen Größen, die Infektionsrate (ir = 0,05) und Heilungsrate (hr = 0,04) halb so groß wie im ersten Diagramm.
Siehe hierzu:
ExcelDateien/Mappe1628d.htm (nur zur Ansicht) oder ExcelDateien/Mappe1628d.xls (herunterladbar und interaktiv) |
| |
|
|
| Beschreibt sodann das Systemverhalten, den Zweck und die Grenzen des betrachteten Modells.
Diskutiert in eurer Kleingruppe auch, welche gesellschaftliche Relevanz Verhaltens- beschreibungen haben, die auf der Grundlage von Simulationen entstanden sind. |
|
In diesem dynamischen Modell der Ausbreitung von Viren nimmt die Zahl der Gesunden in der ersten Zeit schnell ab und nähert sich dann langsam immer mehr der Null. Alle Gesunden werden krank. Die Zahl der Kranken steigt schnell auf einen Höchstwert, nicht ganz halb so groß, wie der Anfangswert der Gesunden. Dann sinkt die Zahl der Kranken - langsamer werdend - auch gegen Null ab. Die Zahl der Immunen steigt zunächst schnell an und strebt dann langsamer werdend einem Höchstwert zu. Dies gilt auch für die Todesfälle. Das folgende Balkendiagramm zeigt, wie sich die Summe aus Immunen und Verstorbenen (in einer logistischen Kurve) der Anfangsgröße der Gesunden nähert.
Siehe hierzu:
ExcelDateien/Mappe1628c.htm (nur zur Ansicht) oder ExcelDateien/Mappe1628c.xls (herunterladbar und interaktiv)
Wird Δt auf 0,3 verkleinert und werden alle anderen Werte wie zuvor beibehalten, so zieht sich der beschriebene Prozess über einen längeren Zeitraum hin, wenn die Interpretation des Zeittaktes Δt = 0,3 = 1Tagbeibehalten wird.
Siehe hierzu:
ExcelDateien/Mappe1628e.htm (nur zur Ansicht) oder ExcelDateien/Mappe1628e.xls (herunterladbar und interaktiv)
Die Modellierung endet also - nach einer quantitativen Phase - mit einer qualitativen Verhaltensbeschreibung. Das ist in diesem Fall aber auch der Zweck des Modells. Es vermittelt eine grundlegende (qualitative) Einsicht aber auch neue, weiterführende Fragen!
Nach einer gewissen Zeitdauer haben wir in den obigen Simulationsergebnissen gleich viel Gesunde und Kranke. Diese Zeitdauern sind aber z.B. bei AIDS in Europa unrealistisch. Daher muss bei der Modellierung einer HIV-Infektion mit Todesfällen neben der Infektions-, Heilungs- und Sterberate auch den Zeittakt berücksichtigt werden. Der Zeittakt gestattet eine Modellierung, die den Prozess verlangsamt, wie es das letzte Diagramm zeigt.
Und auch die Raten hängen nicht nur vom Typ der Epidemie ab, sondern auch davon ab, in wie weit die jeweilige Bevölkerung „aufgeklärt“ ist. Die Raten für AIDS sind z.B. in Afrika und Deutschland sehr unterschiedlich. Hier zeigen sich erneut die Grenzen des Modells. Sie können und sollten selbsttätig mit der Untersuchung von Szenarien überschritten werden.
Eine Analyse der AIDS-Fälle in unterschiedlichen Ländern zeigt, dass sich das HI-Virus in einigen afrikanischen Ländern nahezu ungehemmt ausbreiten kann. Das aber bedeutet eine Vergrößerung der Infektionsrate. Und daraus, dass in diesen Ländern die teuren Medikamente gegen AIDS kaum bezahlbar sind, folgt eine Vergrößerung der Sterberate.
Die Bedeutung der vorstehenden Simulationsergebnisse für die Welt-Gesellschaft liegt also darin, dass erstens eine Aufklärung sowie zweitens ein sicherer Schutz gegen die Ausbreitung des HI-Virus notwendig sind. Rote Beete helfen nicht! |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |





















