| |
|
|
Definition der
empirischen Varianz s²
Für  kann man auch schreiben: m(x) Mittelwert der Größe x kann man auch schreiben: m(x) Mittelwert der Größe x
|
|
s² =
(Summe aller Abweichungsquadrate) geteilt durch (Anzahl der Beobachtungswerte)
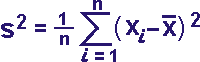
Die Formel in anderer Symbolik:
s(x)² = 1/n ∑ [x(i) - m(x)]² für i = 1 bis n |
| |
|
|
|
|
|
Zur Berechnung der Varianz brauchen wir das arithmetische Mittel m(x).
m(x) = (1,30 + 1,34 + 1,35 + 1,38 + 1,39 + 1,39 + 1,40 + 1,40 + 1,40 + 1,44 + 1,45 +
1,48 + 1,52) : 13 = 1,403 (abgerundet ) |
| |
|
|
Berechnung der empirischen Varianz zum Merkmal
"Körpergröße x " der Jungen gemessen in m |
|
Name |
Index |
Körpergröße x |
[x(i) - m(x)]² |
| Michail |
1 |
1,40 |
|
| Tarik |
2 |
1,45 |
0,0025 |
| Lars |
3 |
1,35 |
0,0025 |
| Christian |
4 |
1,39 |
0,0001 |
| Devin |
5 |
1,39 |
0,0001 |
| Brian |
6 |
1,30 |
0,01 |
| Julian |
7 |
1,34 |
0,0036 |
| Marco |
8 |
1,44 |
0,0016 |
| Simon |
9 |
1,38 |
0,0004 |
| Marc P. |
10 |
1,40 |
≈ 0 |
| Jeron |
11 |
1,40 |
≈ 0 |
| Mario |
12 |
1,52 |
0,0144 |
| Marc W. |
13 |
1,48 |
0,0064 |
Summe |
18,24 |
0,0416 |
Mittelwert / Varianz |
|
≈ 0,0032 |
|
| |
|
|
Warum wird die Abweichung
[x(i) - m(x)] quadriert? |
|
Das Quadrieren der Abweichungen vom Mittelwert hat zur Folge, dass sehr kleine Abweichungen vom arithmetischen Mittel kaum zur Geltung kommen. Große Abweichungen jedoch sehr stark ins Gewicht fallen. Je kleiner also die Varianz ist, je geringer ist die Streuung. Je größer die Varianz ist, je größer ist die Streuung. |
| |
|
|
Definition der empirischen Standardabweichung |
|
Die Standardabweichung s ist die positive Wurzel aus der empirischen Varianz.
s = √s²
Für das Merkmal "Körpergröße x" Jungen beträgt die Standardabweichung
s ≈ 0,056
Die Standardabweichung hat dieselbe Maßeinheit wie die Beobachtungswerte. Deshalb eignet sie sich besser zum direkten Vergleich mit den Daten der Stichprobe. Ihre Interpretation ist die gleiche, wie bei der Varianz. |
| |
|
|
Excell-Mappen
zur Ansicht im Browser |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm..." öffnet sich im Browser eine Excel-Mappe zu Ansicht. Sie ist nicht interaktiv. Im Internet Explorer (ältere Version) kann sie mit Datei öffnen mit Microsoft-Excel in eine interaktive verwandelt werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Ansichtsseite schließt. |
Interaktive Excell-Mappen
im Browser öffnen |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm ... " öffnet sich im Browser ein Fenster zum Dateidownload. Mit "öffen" aktivieren und OK wird die Excel-Mappe geöffnet und ist interaktiv. Sie kann auch auf den eigenen Rechner geladen werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Excel-Mappe schließt. |
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
- Berechnet das arithmetische Mittel und bestimmt den Median zum Merkmal "Körpergröße y " bei den Mädchen.
- Vergleicht die arithmetischen Mittel und Mediane der Mädchen und Jungen miteinander. Was könnt ihr feststellen? Sind die Mädchen oder die Jungen größer?
- Berechnet die empirische Varianz und die Standardabweichung für die Körpergröße y der Mädchen.
|












