Bei einer Regression
(lat. Rückgang, Annäherung)
suchen wir eine Funktion
für die die Summe aller µ(i)
minimal ist.
Eine Einschränkung auf lineare Funktionen ist dabei eine verbreitete Annahme.
Sie ist auch aus praktischer Erfahrung plausibel, weil zwischen den Merkmalen häufig ein linearer Zusammenhang besteht.
Dann sprechen wir von einer
linearen Regression:
|
|
 |
| |
|
|
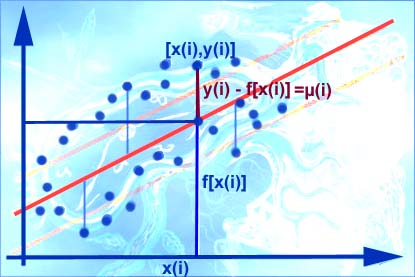
Wir suchen also eine
lineare Funktion
f(x) = a + b · x
deren Gerade die Punkte eines Streudiagramms bestmöglich annähert.
|
|
Zum Zweck der Regression (Annäherung) einer "Punktwolke" durch eine Gerade, suchen wir das Minimum der folgenden Funktion F(a/b) mit zwei Variablen:
F(a/b) = ∑ µ(i)² = ∑ {y(i) - f[x(i)] }² =
∑ {y(i) - [a + b·x(i)] }² für i von 0 bis n
Wir quadrieren die Abstände µ(i), dann gibt es nur positive Werte. Bilden die Summe aller µ(i)² und suchen das Minimum für diese "quadratische Funktion". Das Minimum finden wir über partielle Ableitungen. |
| |
|
|
| |
|
So finden wir die lineare Regressions-Funktion
f(x) = a + b · x mit
b = s(xy) / s(x)² und a = m(y) - b · m(x)
s(xy) = m(x·y) - m(x)·m(y) und
s(x)² = 1/n ∑ [x(i) - m(x)]² für i = 1 bis n
|
| |
|
|
Excell-Mappe
zur Ansicht im Browser |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm..." öffnet sich im Browser eine Excel-Mappe zu Ansicht. Sie ist nicht interaktiv. Im Internet Explorer (ältere Version) kann sie mit "Datei öffnen mit Microsoft-Excel" in eine interaktive verwandelt werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Ansichtsseite schließt. |
Interaktive Excell-Mappe
im Browser öffnen |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm ... " öffnet sich im Browser ein Fenster zum Dateidownload. Mit "öffen" aktivieren und dann OK wird die Excel-Mappe geöffnet und ist interaktiv. Sie kann auch auf den eigenen Rechner geladen werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Excel-Mappe schließt. |
| |
|
|
Hinweis auf weitere Regressionsmodelle |
|
In manchen Situationen ist eine lineare Regression nicht geeignet. Dies kann dann der Fall sein, wenn sich das Datenmaterial im Streugeigramm augenscheinlich anders darstellt, oder wenn Modelle einen nichtlinearen Zusammenhang von Merkmalen postulieren. In diesen Fällen sind dann andere Regressionsfunktionen (quadratische, exponentielle...) anzuwenden. Darauf wird hier aber nicht eingegangen. |
| |
|
|
  |
|
     |
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
- Leitet die Form für die lineare Regression schrittweise her, falls ihr partielle Ableitungen bilden könnt.
- Es gibt auch eine Herleitung über die Scheitelpunktsform einer quadratischen Funktion.
Aber Achtung: Die Herleitungen sind nicht trivial!
|












