|
|
 |
| |
|
|
1. Dazu werden die Paare
(Energieverbrauch /
CO2-Konzentration )
in einer Tabelle zusammengestellt.
Die Werte stammen aus den zuvor gegebenen Datensätzen.
|
|
Jahr |
Index |
Energieverbrauch EU (27)
in 1000.000 tRÖE |
CO2-Konzentration
in ppm |
1994 |
1 |
1043,894 |
359 |
1995 |
2 |
1065,549 |
359 |
1996 |
3 |
1111,596 |
363 |
1997 |
4 |
1100,106 |
363 |
1998 |
5 |
1106,587 |
367 |
1999 |
6 |
1102,294 |
367 |
2000 |
7 |
1108,274 |
368 |
2001 |
8 |
1134,822 |
371 |
2002 |
9 |
1122,837 |
373 |
2003 |
10 |
1155,628 |
375 |
2004 |
11 |
1171,482 |
377 |
2005 |
12 |
1165,876 |
380 |
|
| |
|
|
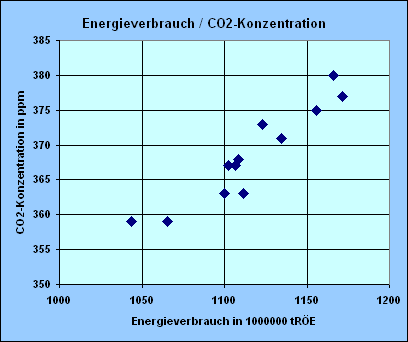
2. Das Streudiagramm
ist eine Möglichkeit die beiden Merkmale gegeneinander
in einem Koordinatensystem darzustellen.
Das Merkmal "Energieverbrauch" wird als erklärende Variable (Einflussfaktor) und das Merkmal "CO2-Konzentration" als abhängige Variable (Zielvariable) gesehen. Also:
x = Energieverbrauch und
y = CO2-Konzentration.
|
|
 |
| |
|
|
Excell-Mappe
zur Ansicht im Browser |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm..." öffnet sich im Browser eine Excel-Mappe zu Ansicht. Sie ist nicht interaktiv. Im Internet Explorer (ältere Version) kann sie mit "Datei öffnen mit Microsoft-Excel" in eine interaktive verwandelt werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Ansichtsseite schließt. |
Interaktive Excell-Mappe
im Browser öffnen |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm ... " öffnet sich im Browser ein Fenster zum Dateidownload. Mit "öffen" aktivieren und dann OK wird die Excel-Mappe geöffnet und ist interaktiv. Sie kann auch auf den eigenen Rechner geladen werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Excel-Mappe schließt. |
| |
|
|
3. Der Korrelationskoeffizient
ist eine weitere Möglichkeit den Zusammenhang zwischen Energieverbrauch und Luftbelastung zu beschreiben. |
|
Der Korrelationskoeffizienten r(xy) ist der Qotient aus der empirischen Kovarianz s(xy) und dem Produkt der Standardabweichungen s(x) und s(y) (siehe Standardabweichungen)
r(xy) = s(xy) / s(x) · s(y) ≈ 0,94
Die Größen Energieverbrauch und Luftbelastung korrelieren sehr stark. Sie stehen in einem nahezu linearen Zusammenhang.
|
| |
|
|
4. Schließlich ist die
lineare Regressionsfunktion
eine Möglichkeit, den Zusammenhang zwischen Energieverbrauch und Luftbelastung zu beschreiben
und darzustellen.
|
|
Wir suchen eine lineare Funktion y = a + bx, deren Gerade sich gut in das obige Streudiagramm einfügt. Die Summe aller Punkt-Abweichungen von der Geraden sollte minimal sein. Das leistet eine Funktion mit den folgenden Parametern:
b = s(xy) / s(x)² und a = m(y) - b · m(x)
s(xy) = m(x·y) - m(x)·m(y) und
s(x)² = 1/n ∑ [x(i) - m(x)]² für i = 1 bis n
Die Einschränkung auf lineare Funktionen ist eine verbreitete Annahme. Sie ist aus praktischer Erfahrung plausibel, weil häufig zwischen den Merkmalen ein linearer Zusammenhang besteht.
|
| |
|
|
Berechnung des Anstiegs b
der Regressionsgeraden
|
|
b berechnet sich als Quotient aus der empirischen Kovarianz s(xy) und der empirischen Varianz s(x)²
b = s(xy) / s(x)² ≈ 0,17
|
| |
|
|
Berechnung des
y-Achsenabschnitts a
der Regressionsgeraden |
|
a berechnet sich als Differenz des Mittelwertes y und dem Produkt von b und Mittelwert von x
a = m(y) - b · m(x) ≈ 179,3 |
| |
|
|
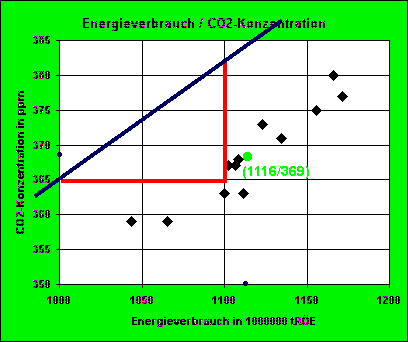
Der rote Winkel zeigt den Anstieg von 0,17 der blauen Geraden.
0,17 = 17/100
das sind:
100 Einheiten nach rechts und
17 Einheiten nach oben.
Legt man nun eine parallele Gerade durch den y-Achsenabschnitt
a = 179,3
oder durch den
Punkt [m(x)/m(y)] ≈ (1116/369), so entsteht die Regressionsgerade. |
|
 |
| |
|
|
Interpreationen
zu den Regressionen |
|
Der Korrelationskoeffizient ist nahezu 1. Das bedeutet: Der Zusammenhang zwischen Energieumsatz und Luftbelastung ist linear.
Die Regressionsgerade erlaubt also eine Prognose, wie viel CO2 bei steigendem Energieverbrauch zu erwarten ist. Das aber nur unter der Annahme, dass die momentanen Technologien zur Energieerzeugung und zum Energieumsatz beibehalten und nicht verbessert werden.
Die Regressionsgerade sagt nichts darüber aus, ob mit dem steigenden CO2 auch die mittlere Jahrestemperatur steigt; sich also das Klima verändert! |
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
Systematisierungen zur Korrelation siehe:
|












