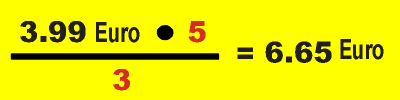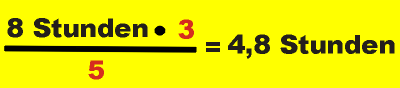|
 |
 |
 |
 |
 |
 |
Schlussrechnen und lineare Funktionen |
 |
 |
 |
 |
 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Letzte Änderung: 05.05.2007 © Pädagogisches Institut für die deutsche Sprachgruppe - Bozen. 2000 - |
 |