|
Exponential-, Logarithmus- und logistische Funktionen
Fallbeispiel für einen Tilgungsplan |
|
 |
|
 |
|
 |
|
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Annahme
und Fragen
|
|
Nehmt einmal an, dass ein stark verschuldetes "armes Land" bei einem Schuldenstand von 15 Millionen US$ keine neuen Schulden mehr machen würde.
Frage 1: Wie lange müsste das Land bei einem Zinssatz von 6% zurückzahlen, wenn es jährlich 2 Millionen US$ zurückzahlen würde?
|
| |
|
|
Definition:
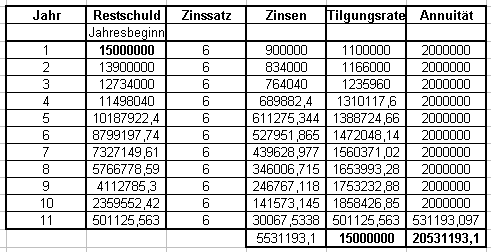
Unter der Annuität versteht man die jährliche Rück-Zahlung. Es ist die Summe aus Zinsen und Tilgung(srate).
Für einen Tilgungsplan gibt es zwei Fälle: |
|
 |
| |
|
|
a) die Annuität wird konstant gehalten, |
|
|
| |
|
|
b) die Tilgungsrate wird konstant gehalten. |
|
Frage 2:
Wie hoch müsste die jährliche Annuität des Landes bei einem Zinssatz von 6% sein, wenn es die Schulden in 10 Jahren abgezahlt haben wollte? |
| |
|
|
|
|
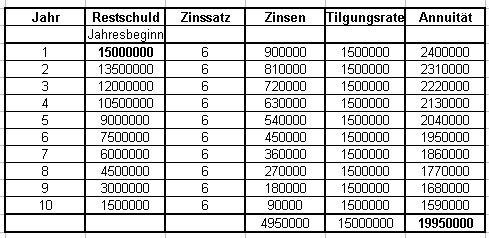 |
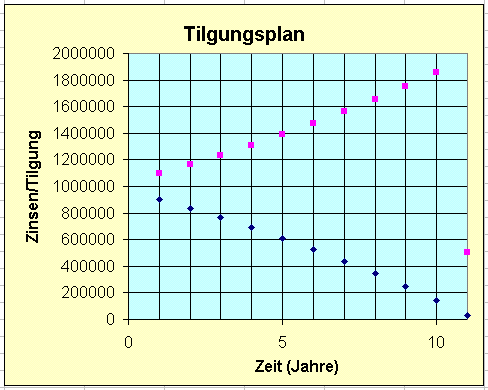
Diagramme zu den obigen Tilgungsplänen |
|
 |
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
- Wie hoch müsste die jährliche Annuität des obigen Landes bei einem Zinssatz von 6% sein, wenn es die Schulden in 10 Jahren abgezahlt haben wollte?
- Nutzt bei eurer Kalkulation das Werkzeug Excel und fertigt auch Diagramme an.
- Experimentiert mit der Tilgung von Schulden beim Kauf eines Moped auf Schuldenbasis.
- Hättet ihr beim Kauf eines Mopeds Bargeld zur Verfügung gehabt, wie viel hättet ihr sparen können?
|
|
|
|
|
|
|
|
|
|
Letzte Änderung: 14.02.2009
© Pädagogisches Institut für die deutsche Sprachgruppe
- Bozen. 2000 -
|
|
|
|
 |
|
|
|
|


















