Beispiel 1:
|
|
Die Kosten k eines Gutes stehen in funktionaler Abhängigkeit (im Zusammenhang) mit der gekauften Menge m des Gutes; wobei der Preis p = 0,60€/1kg eine Konstante sein soll. |
| |
|
|
Darstellung
der Abhängigkeit
als
Zuordnung |
|
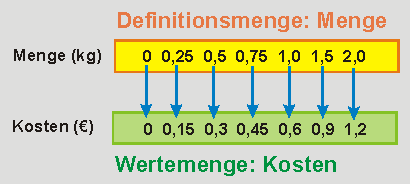
Zuordnung lenkt den Blick darauf, dass die Menge m und die Kosten k eines gekauften Gutes mittels einer Abbildung zwischen einer Definitionsmenge und einer Wertemenge dargestellt werden kann. Die Abbildung wird durch Pfeile verdeutlicht. |
| |
|
|
| |
|
 |
| |
|
|
Darstellung
der Abhängigkeit
als Wertetabelle
(oder Wertetafel) |
|
Menge (kg) |
0 |
0,25 |
0,5 |
0,75 |
1 |
1,5 |
2 |
... |
Kosten (€) |
0 |
0,15 |
0,30 |
0,45 |
0,60 |
0,90 |
1,20 |
... |
In der Wertetabelle sind die zugeordneten Werte als Wertepaare (Menge/Kosten) dargestellt. |
| |
|
|
Darstellung
der Abhängigkeit
als
Term
|
|
Kennt man aber die gekaufte Menge m und den konstanten Preis p, so kann man die Kosten k mittels einer Rechenvorschrift berechnen:
Die Menge m wird mit dem konstanten Preis p multipliziert |
m · p |
Rechenvorschriften, ob sie sprachlich formuliert sind oder als Formen mit Variablen (Leerstellen) ausgedrückt werden, nennt man Term. Geläufig ist auch der Begriff Zuordnungsvorschrift. Er bedeutet inhaltlich dasselbe wie Rechenvorschrift. |
| |
|
|
Beispiel 2:
|
|
Die Fläche I eines Quadrats steht in funktionaler Abhängigkeit zu (im Zusammenhang mit) seiner Seitenlänge a |
| |
|
|
Darstellung
der Abhängigkeit
als Zuordnung |
|
Zuordnung lenkt den Blick darauf, dass die Seitenlänge a und der Flächeninhalt I eines Quadrates mittels einer Abbildung zwischen einer Definitionsmenge und einer Wertemenge dargestellt werden kann. Die Abbildung wird durch Pfeile verdeutlicht. |
| |
|
|
|
|
|
| |
|
|
Darstellung
der Abhängigkeit
als Wertetabelle
(oder Wertetafel) |
|
Seitenlänge (cm) |
0 |
0,25 |
0,5 |
0,75 |
1 |
1,5 |
2 |
... |
Flächeninhalt (cm²) |
0 |
0,0625 |
0,25 |
0,5625 |
1 |
2,25 |
4 |
... |
In der Wertetabelle sind die zugeordneten Werte als Wertepaare (Seitenlänge/Inhalt) dargestellt. |
| |
|
|
Darstellung
der Abhängigkeit
als
Term |
|
Kennt man aber die Seitenlänge a, so kann man den Flächeninhalt I mittels einer Rechenvorschrift berechnen:
Die Seitenlänge a des Quadrates wird mit
sich selbst multipliziert |
a² |
Rechenvorschriften, ob sie sprachlich formuliert sind oder als Formen mit Variablen (Leerstellen) ausgedrückt werden, nennt man Term. Geläufig ist auch der Begriff Zuordnungsvorschrift. Er bedeutet inhaltlich dasselbe wie Rechenvorschrift. |
| |
|
|
|
Beispiel 3:
|
|
Der Weg s steht in Abhängigkeit zur (im Zusammenhang mit der) Fahrtzeit t; wobei die Geschwindigkeit v = 40km/1h konstant bleiben soll. |
| |
|
|
Darstellung
der Abhängigkeit
als Zuordnung |
|
Zuordnung lenkt den Blick darauf, dass die Fahrtzeit t und der in dieser Zeit gefahrene Weg s bei konstanter Geschwindigkeit mittels einer Abbildung zwischen einer Definitionsmenge und einer Wertemenge dargestellt werden kann. Die Abbildung wird durch Pfeile verdeutlicht. |
| |
|
|
|
|
|
| |
|
|
Darstellung
der Abhängigkeit
als Wertetabelle
oder Wertetafel |
|
Fahrtzeit (h) |
0 |
0,25 |
0,5 |
0,75 |
1 |
1,5 |
2 |
... |
Weg (km) |
0 |
0,0625 |
0,25 |
0,5625 |
1 |
2,25 |
4 |
... |
In der Wertetabelle sind die zugeordneten Werte als Wertepaare (Fahrtzeit/Weg) dargestellt. |
| |
|
|
Darstellung
der Abhängigkeit
als
Term |
|
Kennt man aber die Fahrtzeit t und die konstante Geschwindigkeit v, so kann man den gefahrenen Weg s mittels einer Rechenvorschrift berechnen:
Die Fahrt-Zeit t wird mit der konstanten Geschwindigkeit v multipliziert |
t · v |
Rechenvorschriften, ob sie sprachlich formuliert sind oder als Formen mit Variablen (Leerstellen) ausgedrückt werden, nennt man Term. Geläufig ist auch der Begriff Zuordnungsvorschrift. Er bedeutet inhaltlich dasselbe wie Rechenvorschrift. |















