Modellierungen an einem Fallbeispiel:
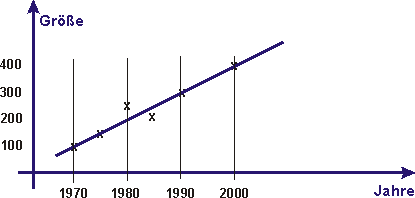
Wir nehmen an, dass sich die Entwicklung einer Größe bis zum Jahr 2000 (Arbeitslosigkeit oder Energieverbrauch oder Artensterben oder ...) mit einem linearen Term annähern ließe. |
|
 |
| |
|
|
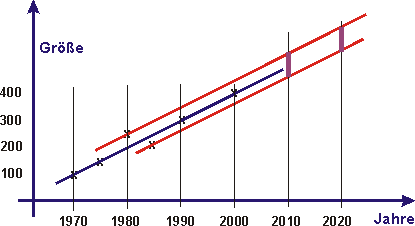
Erste Modellierung
Die Unsicherheit der Entwicklung für die Jahre 2010 und 2020 könnte durch zwei Parallelen (rot) zur Entwicklungsgerade (blau) bis zum Jahr 2000 beschrieben werden. Die violett dargestellten Intervalllängen wären dann ein Maß für die Unsicherheit. |
|
 |
| |
|
|
| |
|
Der Quotient dieser Intervalllängen (violett) durch die Ordinaten der Entwicklungsgerade im Jahr 2010 und 2020 wären eine Zahl zwischen 0 und 1. Sie könnten als Wahrscheinlichkeit gedeutet werden. Aber: Die so berechnete Unsicherheit der Prognose für 2010 wäre größer als die Unsicherheit der Prognose für 2020. Die so gedeutete Unsicherheit würde also mit zunehmender Zeit abnehmen. Und das widerspricht jeder Erfahrung. Daher ist diese Modellierung ungeeignet. |
| |
|
|
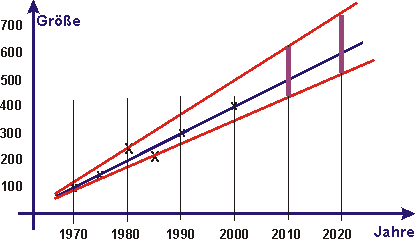
Zweite Modellierung
Die Unsicherheit der Entwicklung für die Jahre 2010 und 2020 könnte wohl besser durch zwei Geraden (rot), die die Abweichungen von der Entwicklungsgeraden berücksichtigen, beschrieben werden. Die violett dargestellten Intervalllängen wären dann wieder ein Maß für die Unsicherheit. |
|
 |
| |
|
|
| |
|
Der Quotient dieser Intervalllängen (violett) durch die Ordinaten der Entwicklungsgerade im Jahr 2010 und 2020 wären eine Zahl zwischen 0 und 1. Sie könnte - wie zuvor - als Wahrscheinlichkeit gedeutet werden. Die so gedeutete Unsicherheit würde also mit zunehmender Zeit zunehmen. Und das würde mit der Erfahrung übereinstimmen. |
| |
|
|
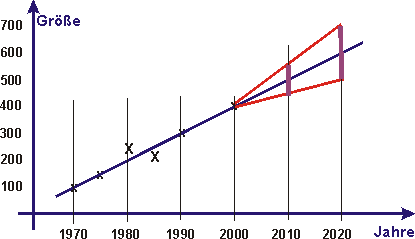
Es bleibt aber die Frage,
ob es nicht noch andere Modelle gibt. Hier eine Anregung.
Die Unsicherheit würde, so wie in nebenstehender Grafik definiert, proportional mit der Zeit zunehmen. Was ist von dieser Modellierung zu halten? Kann sie begründet werden? |
|
 |
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
- Beschäftigt euch mit der Modellierung der Unsicherheit einer Prognose, wenn sich die Entwicklung einer Größe bis zum Jahr 2000
a) mit einem quadratischen Term annähern ließe und
b) mit einem exponentiellen Term annähern ließe.
- Diskutiert den Fall, dass die Wahrscheinlichkeit für die Unsicherheit 1 ist.
Was bedeutet dies?
Kann das in obigen Modellen der Fall sein?
|
















