CAS-Werkzeug: Derive
Eine quadratische Funktionsgleichung finden

Am Beispiel der Ponto de Cecco und des mit Transparent- Millimeterpapier abstrahierten Bogens und der daran abgelesen Wertetabelle, wird in der Folge gezeigt, wie mit Derive die konkrete Funktionsgleichung gefunden werden kann.

Abfolgeschritte

1. Eingabe der Funktionsvorschrift mit Parametern

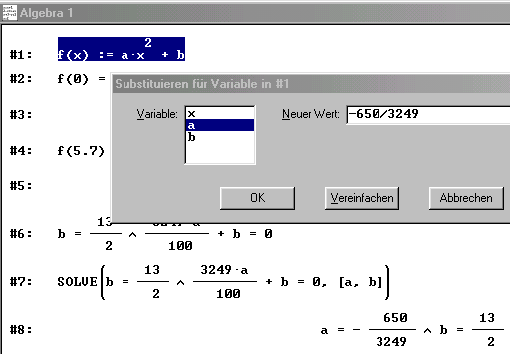
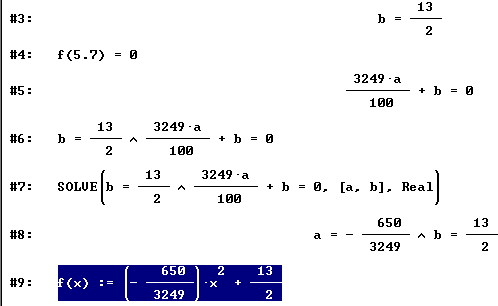
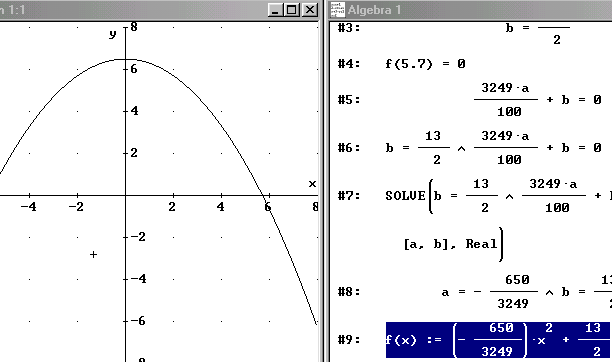
Nach Eingabe der Funktion #1: werden nun nacheinander die beiden abgelesenen Koordinatenpaare (0/6.5) und (5.7/0) über die Eingabezeile eingegeben.
(0/6.5) kann geschrieben werden: f(0) = 6.5. Das bedeutet, der Funktionswert an der Stelle 0 ist 6.5.

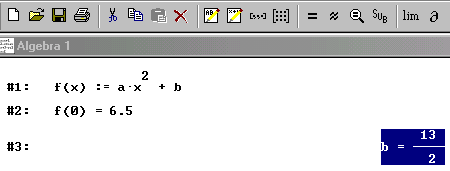
Eingabe: "f(0) = 6.5" erzeugt die Zeile #2: ... f(0) = 6.5

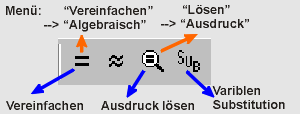
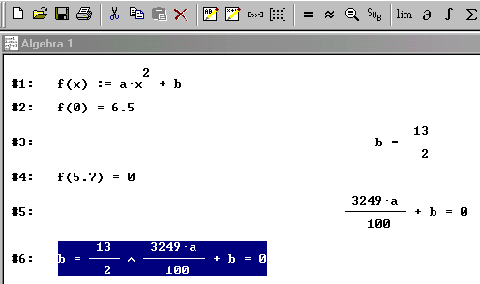
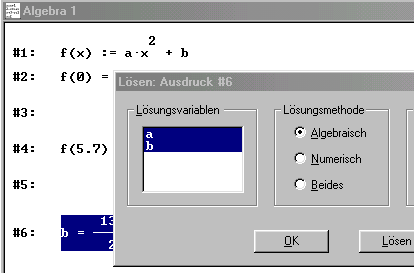
Ein Klick auf das Symbol "Vereinfachen" erzeugt die Zeile #3: b = 13/2 (oben blau unterlegt). Analog erfolgt die Eingabe und Vereinfachung für das zweite Koordinatenpaar.

3. Eingabe eines Gleichungssystems oder einer Rechenbedingung

In die Eingabezeile wird nun für die Gleichungen #3 sowie #5 eine Und-Bedingung formuliert. Beide Gleichungen sollen zugleich erfüllt werden.
Eingabe: #3 und #5 wobei die Tastatur für das logische "und" ein Zeichen verfügbar macht. Es sollte genutzt werden.
Die Zeile #6 (nebenan blau unterlegt) entsteht.

Ein Klick auf das Symbol "Ausdruck lösen" öffnet das nebenstehende Fenster. Hier werden mit Shift die Variablen a und b als Lösungsvariable gefordert und die Lösungsmethode "Algebraisch" sowie der "Lösungsbereich" reell aktiviert. Sodann wird auf Lösen geklickt.

5. Anzeige der Lösung des Systems

In Zeile #7 wird mit SOLVE noch einmal angezeigt, was unter welchen Bedingungen gelöst werden soll. Mit demselben Schritt wird aber auch die Zeile #8 erzeugt.
Das sind jetzt die konkreten rationalen Zahlen für die Formvariablen der gesuchten Funktion.

6. Eingeben von Zahlen in die Formvariablen

Die Funktion #1 wird aktiviert (blau unterlegt). Ein Klick auf das Symbol SUB (Variablen Substitution)
öffnet das nebenstehende Fenster. Hier wird die Variable a aktiviert (blau unterlegt) und bei "Neuer Wert" die gefundene Lösung für a (siehe #8) eingetippt.

Dann wird b aktiviert und ebenfalls die gefunden Lösung eingegeben.
Dann erst wird OK gedrückt.
Die Zeile #9 erscheint. Sie zeigt jetzt die konkrete Gleichung für die gesuchte Funktion.