Dieser Rechner hat ein Computer-Algebra-System integriert (CAS). Der Handheld fällt durch seine sehr intuitive Bedienung ins Auge. Das große LCD mit seiner Touch-Funktion unterstreicht diesen Eindruck sofort. Ob mit einem Stift oder mit dem Finger, schnell ist man mit den übersichtlichen Menüs vertraut und kommt schnell zu einer Lösung.

Durch die Größe des Displays ist eine Übersichtlichkeit zu jedem Zeitpunkt gegeben. Das Display bzw. die Anzeige lässt sich in einigen Anwendungen drehen, so hat man noch mehr Platz für aufwendige Terme oder große grafische Darstellungen.

Durch die aus- und einblendbare "virtuelle Tastatur" bleibt der Rechner von Doppel-, Dritt- oder gar Viertbelegungen verschont.

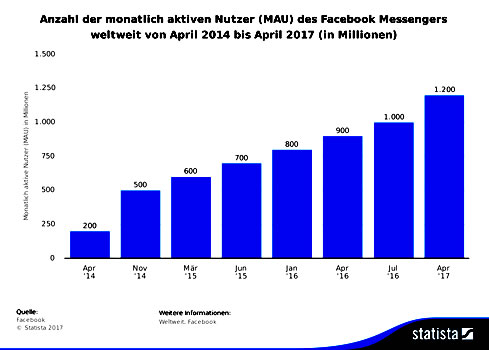
Ein Beispiel: Angenommen wir interessieren uns für die Anzahl der monatlich aktiven Nutzer des Facebook-Messengers weltweit. Unter der Adresse

https://static.giga.de/wp-content/uploads/2017/05/anzahl-der-monatlich-aktiven-nutzer-des-facebook-messengers-weltweit-bis-april-2017.png

finden wir hierzu einige Zahlen. Die Grafik ist allerdings etwas irreführend, da die Zeitintervalle auf der Rechtsachse unterschiedlich groß sind.

Im Hauptmenü des Rechners wählen wir das Unterprogramm Statistik. In die erste Liste übetragen wir die Zeitangaben. Die zweite Liste betiteln wir mit dem Buchstaben t für die Zeit. Ausgehend vom 1. Januar 2014 wären Ende April 2014 vier Monate d. h. 0,333 Jahre vergangen, Ende November 2014 11 Monate, d.h. 0,92 Jahre u.s.w.

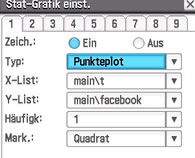
Wir wählen in der Menüzeile den Punkt Grafik einst und nehmen die folgenden Einstellungen vor:

Im Auswahlmenü oberhalb der Tabelle wählen wir durch den Graphmodus.

Die Anordnung der Punkte legt ein lineares Modell nahe. Es könnte sich aber auch um ein logistisches Wachstum handeln, welches für die kommenden Jahre einem Sättigungswert zustrebt. Dies scheint plausibel, da die Anzahl der möglichen Nutzer weltweit schließlich nach oben beschränkt ist.

Wir wählen den Menüpunkt CALC und dort den Unterpunkt Regressionen. Nun werden uns eine ganze Reihe von Modellen angeboten.

Wir entscheiden uns für Logistische Reg. und nehmen die folgenden Einstellungen vor:

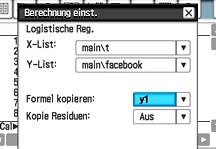Der Rechner ermittelt nun eine logistische Funktion, die möglichst wenig von den gewählten Punkten abweicht. Hier die berechneten Funktionsparameter:

Die Funktion hat damit die folgende Formel:

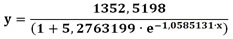
Mit ihr können wir nun Prognosewerte für die folgenden Jahre berechnen.

Das geht so:

Im Auswahlmenü oberhalb der Tabelle öffnen wir mit die Liste aller Funktionsgleichungen.

Zunächst klicken wir den Term hinter y1 = an, markieren mit Datei / alles auswählen den ganzen Term und kopieren ihn mit kopieren in die Zwischenablage. Anschließen geben wir einer neuen Spalte den Titel 'Modell' und klicken auf das Feld zur Eingabe eines Terms am Fuß der Liste. Nun klicken wir in das Eingabefeld hinter 'Cal =' und wählen Edit / einfügen.

Der Funktionsterm wird in das Feld übertragen. Abschließend ersetzen wir den Variablennamen x durch t.

Ein Druck auf EXE und die Werte der Modellfunktion werden in die Tabelle eingetragen.

Angenommen, uns interessieren die Zahlen der monatlich aktiven Nutzer des Facebook-Messengers für die Jahre 2018, 2019 und 2020. Und zwar jeweils im April.

Wir ergänzen dann unsere Tabelle in der nebenstehenden Weise.

Dann klicken wir auf das Feld am Fuß der Wertetabelle unserer Modellfunktion und anschließend zweimal auf den Term hinter Cal=. Die Wertetabelle wird neu berechnet und zwar auch für die neuen t-Werte.

Wir kehren noch einmal zur Ausgangssituation zurück. Nun lassen wir allerdings mit der Berechnung der Modellfunktion die Residuen der beiden Modellfunktionen jeweils in einer Liste anzeigen. Das geht über die folgende Einstellung:

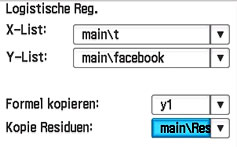
Unter Residuen versteht man die Abweichungen der modellierten Werte von den tatsächlichen Werten. Die können positiv oder negativ sein. Liegen die realen Werte unter der Modellfunktion sind sie negativ, sonst positiv.

In der nebenstehenden Tabelle sind diese Abweichungen (Residuen) sowohl für das logistische Modell (ResLogM) als auch für das lineare Modell (ResLinM) aufgelistet.

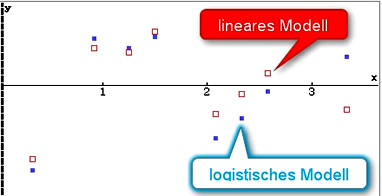
Über den Menüpunkt Grafik einst legen wir nun fest, dass diese beide Listen als Punkteplot dargestellt werden sollen. Durch Wahl von erhalten wir das nebenstehende Diagramm. (Oder ein ähnliches, je nachdem welche Punktdarstellung ihr gewählt habt.) Ein solches Diagramm heißt Residuendiagramm. Wir sehen: In 6 von 8 Fällen liegt das rot-weiße Quadrat etwas näher an der Rechtsachse als das blaue. Die Abweichungen dieses Modells von den gemessenen Werten sind also etwas kleiner. Somit stellt das lineare Modell die etwas bessere Modellierung dar.

Kurzfristig spricht auch einiges dafür, da Ende September 2017 bereits 1,6 Mrd. Menschen weltweit Facebook nutzten.

Eine gute Übersicht über die verschiedenen Standardmodelle, die zur funktionalen Modellierung von realen Situationen herangezogen werden können, findet man in:

J. Engel, Anwendungsorientierte Mathematik: Von Daten zur Funktion, Springer-Verlag, 2010