|
|
|
|
|
|
| |
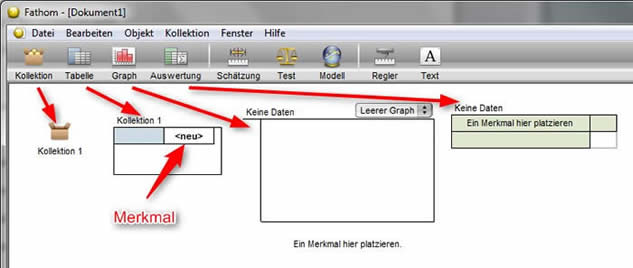
Das Programm FATHOM bietet die Möglichkeit, beliebige Datenreihen auf vielfältige Weise und sehr
komfortabel auszuwerten. Nach Aufruf des Programms öffnet sich ein Fenster, in das die einzelnen Werkzeuge mit der Maus hineingezogen werden können. |
|
 |
| |
Die einzelnen Arbeitsschritte zur funktionalen Modellbildung mit FATHOM sollen hier zur besseren
Veranschaulichung anhand eines Beispiels erläutert werden. Nehmen wir an, wir wollen uns über die
(zukünftige) Entwicklung der Kinderarmut in Deutschland ein Bild machen.
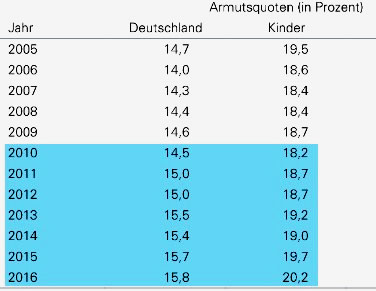
Auf der Seite https://www.boeckler.de/pdf/wsi_vm_armutsquoten_kinder_aeltere.pdf
finden wir Daten über die relative Einkommensarmut (in Prozent) von Kindern in Deutschland
für den Zeitraum von 2010 bis 2016. |
| |
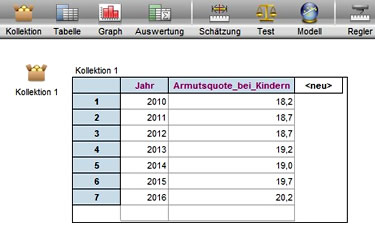
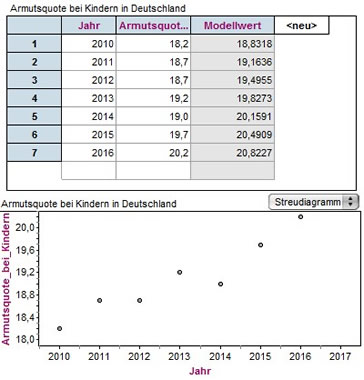
Wir ziehen eine Kollektion in den Arbeitsbereich sowie eine Tabelle.Wir klicken den Namen des ersten Merkmals (<neu>) an und ändern ihn durch die Merkmalsbezeichnung 'Jahr'.
Ähnlich verfahren wir mit mit dem zweiten Merkmal.
In diese Tabelle können wir nun die entsprechenden Werte eintragen.
Hinweis: Es lassen sich auch beliebige Datenreihen mit CTRL-C in die Ablage kopieren und durch Rechtsklick auf die Kollektion / Menüpunkt 'Fälle einfügen' in die Tabelle übertragen.
Hierbei muss man aber darauf achten, dass Dezimalzahlen durch einen Punkt und nicht durch ein Komma markiert sind.
|
|
|
|
|
|
| |
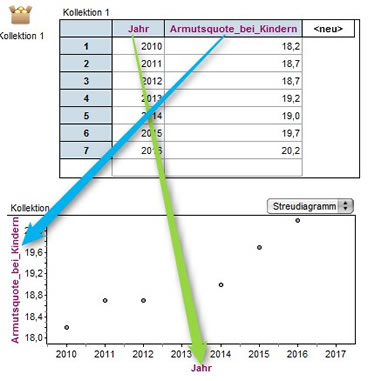
Wir ziehen nun einen leeren Graph in das Fenster. In der Tabelle klicken wir auf das Merkmal 'Jahr' und ziehen dieses bei gedrückter Maustaste zur x-Achse des Koordinatensystems.
Analog verfahren wir mit dem zweiten Merkmal. Dieses ziehen wir zur y-Achse.
Wir erhalten ein Streudiagramm der Datenreihe. |
|
|
|
|
|
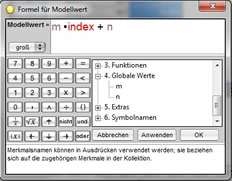
Nun legen wir ein passendes funktionales Modell fest, welches das zeitliche Verhalten dieser Datenreihe
d. h. der Armutsquote bei Kindern in Deutschland beschreiben soll.
Die dritte Merkmalsspalte erhält den Namen 'Modellwert' .
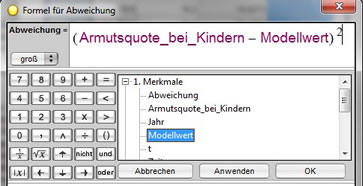
Durch Rechtsklick auf t und Auswahl des Menüpunktes 'Formel bearbeiten' erhalten wir das folgende Fenster:
 |
|
|
| |
|
|
|
Da die Werte für m und n noch nicht festliegen, steht in der Datenliste:
#Name nicht erkannt.
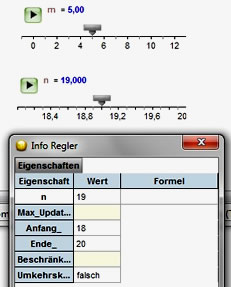
Das werden wir nun durch zwei Regler für m und n
beheben.
Diese ziehen wir auf unsere Arbeitsfläche und geben ihnen durch Doppelklick die Namen m und n.
Klickt man auf den Regler selbst, öffnet sich jeweils ein neues Fenster, in dem Anfangs- und Endwert
für den Regler festgelegt werden können:
|
|
|
| |
|
|
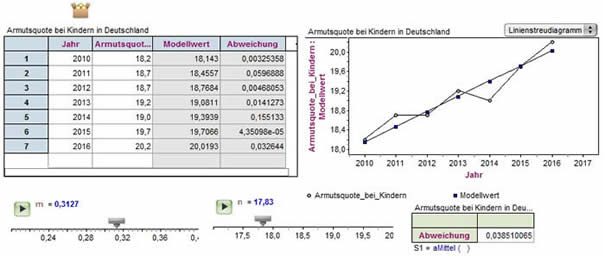
In 6 Jahren ist der Anteil der von Kinderarmut betroffenen Kinder und Jugendlichen um 2% gestiegen. m beträgt also im Mittel 2/6 = 1/3. Wir legen daher für m den Bereich zwischen 0,2 und 0,4 fest.
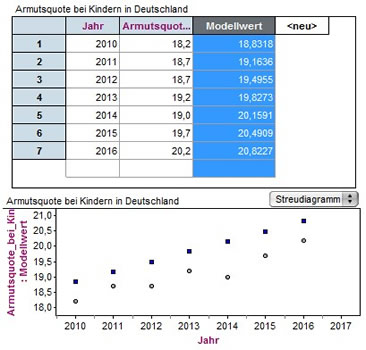
Wir klicken nun in der Tabelle das Merkmal 'Modellwert' an und ziehen es bei gedrückter Maustaste auf die
y-Achse des Streudiagramms.
Dort erscheint ein Pluszeichen, auf das wir den Merkmalsnamen ziehen. Verändern wir nun mit den Reglern die Werte für m und n können wir die Modellfunktion optimal anpassen.
Wie gut diese Anpassung unserer Modellfunktion an die vorgegebenen Werte ist, messen wir durch ein neues Merkmal mit dem Namen 'Abweichung'.
|
|
|
| |
|
|
Den Unterschied zwischen zwei Werten erhält man, indem man die beiden Werte subtrahiert. Nun kann diese Differenz mal positiv oder mal negativ sein. Damit die Werte immer positiv sind, werden sie daher alle quadriert.
FATHOM berechnet also nun für jeden Modellwert die Abweichung vom realen Wert. Bilden wir von allen diesen Werten nun den Mittelwert, so haben wir ein Maß für die Abweichung der Modellfunktion von den realen Werten.
|
|
|
| |
|
|
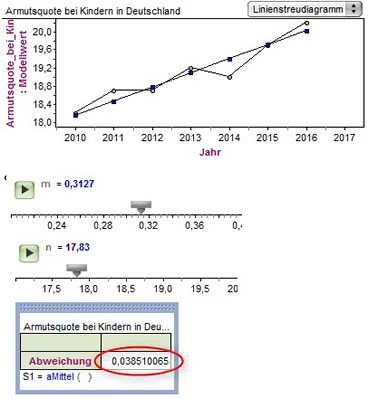
Die Berechnung des Mittelwertes kann FATHOM für uns erledigen.
Dazu ziehen wir eine Auswertung auf unsere Arbeitsfläche. Das Merkmal 'Abweichung' ziehen wir in diese Auswertung:

Der angegebene Wert entspricht dem Mittelwert aller Abweichungen.
Mit den
beiden Reglern stellen wir nun die Werte für m und n so ein, dass der Mittelwert aller Abweichungen
(die Varianz) möglichst klein wird. die Werte die wir jetzt für m und n ablesen, sind die optimalen Werte für unsere Modellfunktion.
In unserem Falle würde diese
y = 0,3127 • x + 17,83 lauten. |
|
|
| |
|
|
Berechnung von Prognosewerten
|
|
Wie verhält es sich mit der Armutbei Kindern und Jugendlichen in Deutschland im Jahr 2020? Um das zu berechnen, setzen wir nun lediglich den Wert 2020 - 2009 = 11 in unsere Modellfunktion ein:
0,3127 • 11 + 17,83 = 21,2697
Ohne tiefgreifende gesellschafts-politische Maßnahmen läge dann also dieser Anteil bei etwa 21,3%.
Im Bundestagswahlkampf 2017 spielte das Thema Armut bei Kindern und Jugendlichen leider keine Rolle.
|
| |
|
Hier noch einmal alle FATHOM-Werkzeuge für diese
Modellierung im Überblick |
 |
| |
|
|
|
|
Nützliche Links |
|
Wer sich intensiver mit dem Programm FATHOM beschäftigen möchte, findet hier wertvolle Informationen: |
| Prof. Biehler, Universität Kassel |
|
http://www.mathematik.uni-kassel.de/~fathom/ |
| Beschreibende Statistik mit FATHOM |
|
https://kobra.bibliothek.uni-kassel.de/bitstream/urn:nbn:de:hebis:34-2007011016602/5/Kadisto8.pdf |
| Unterrichtsprojekte auf der amerik. Seite von FATHOM |
|
http://fathom.concord.org/resources/free-fathom-activities-and-resources/ |
| Sammlung von Datensätzen zu einer ganzen Reihe von Anwendungsmöglichkeiten |
|
http://www.seattlecentral.edu/qelp/Data.html |
| Erste Schritte mit FATHOM (engl.) |
|
http://mathforum.org/pcmi/hstp/resources/leonardo/LeoTeacher_TeacherTrainingModule.pdf |
| |
|
|
| |
|
|
|
|