Anforderungen /
Aufgaben |
|
Mögliche "Lösungen" der Anforderung,
bezogen auf die Klassen (8) 9 und 10 |
| |
|
|
Hinweise:
Die Bearbeitung der folgenden Aufgabe kann Teil einer Gesamtlösung von mehreren arbeitsteilig arbeitenden Kleingruppen sein.
Beschreibung
der
erwerbaren
mathematischen Kompetenzen |
|
Die folgende Lösung zur Konstrukltion und Simulation der dynamischen Aufheizung eines "Glaspalastes" kann in einer Teilgruppe der Klasse erarbeitet werden. Sie kann Teil einer Gesamtlösung sein, bei der andere Gruppen der Klasse parallel an weiteren Modellierungen zum Problem des Wärmeaustausches an Häusern arbeiten. Nach der Präsentation der Gruppenlösungen in der Klasse werden gemeinsam Folgerungen erarbeitet und diskutiert.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 4 Schulstunden notwendig, wenn Teile dieser Arbeiten auch als Hausarbeit angefertigt werden. Für die Besprechung aller Analysen in der Klasse sind dann noch einmal ca. 2 Schulstunden notwendig.
|
| |
|
|
|
|
|
|
|
Konstrukltion und Simulation
der dynamischen Aufheizung eines "Glaspalastes" |
| |
|
|
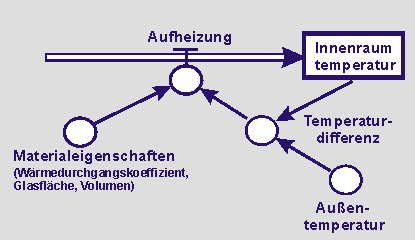
Beschreibt ein Flussdiagramm für ein Aufheizmodell, das schließlich die Verhältnisse so zeigt, wie sie in der Versuchsreihe beschrieben sind.
|
|
|
|
|
|
| Erstellt die Zustands- und Modellgleichung. |
|
Wir beginnen mit einem einfachen Aufheizmodell. In diesem Modell ist die Innenraumtemperatur T die Zustandsgröße und die Aufheizung A die Flussgröße. Die Außentemperatur TA und die Materialeigenschaft m sind Konstante.
Die Zustandsgleichung und die Modellgleichung für die Flussgröße formulieren wir unter Berücksichtigung eines Zeittaktes zwischen Zustand_neu und Zustand_alt aus dem Flussdiagramm heraus. |
| |
|
|
| |
|
T_neu < -- T_alt + Δt · A
Ausgangsgröße Temperatur T = 10 (Grad Celsius);
Δt = 0,1 (Zeittakt = 6 Sekunden)
A = (TA - T) · m mit m = 0,5 und TA = 48 (Grad Celsius) |
| |
|
|
| Programmiert das Aufheizmodell in Excel |
|
Siehe hierzu:
ExcelDateien/Mappe1433a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1433a.xls (herunterladbar und interaktiv) |
|
|
|
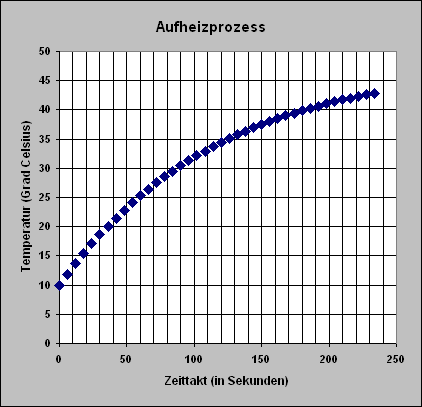
Simuliert das Modell
Das Simulationsergebnis entspricht den oben eingegebenen Anfangsgrößen, den Konstanten
sowie dem Zeittakt. |
|
 |
|
|
|
Beschreibt das Verhalten, den Zweck und die Grenzen des Modells.
Besprecht miteinander, was euch bereits dieses einfache Aufheizmodell sagt, wenn ihr mit verschiedenen Anfangsgrößen und Materialeigenschaften "spielt". |
|
Der Aufheizprozess ist nicht linear! Je kleiner die Temperaturdifferenz zwischen Innen und Außen wird, je geringer ist die Zunahme der Temperatur im Innenraum. Und mit größer werdender Materialeigenschaft m wird innerhalb kürzerer Zeit im Innenraum nahezu die Außentemperatur erreicht.
Diese Einsichten gewinnen wir bereits an diesem einfachen Modell. Und das ist für uns zunächst der Zweck des Modells.
Soll das Modell für technische Entscheidungen zur Energieeffizienz genutzt werden, muss die Materialeigenschaft genauer analysiert und beschrieben werden. Das ist die Grenze in dem bisher untersuchten Modell.
Erweiterte Modell müssten also die Struktur und den Aufbau der Außenhaut eines Gebäudes berücksichtigen.
|
| |
|
|
| Verschriftlich eure Ergebnisse und erstellt eine Präsentation. |
|
Wesentliche Ergebnisse sind in den ExcelMappen dargestellt. Interpretationen sind im vorstehenden Text zu finden. |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |














