| |
|
|
Wortmodell |
|
Ein stark verschuldetes "armes Land" macht bei einem hohen Schuldenstand keine neuen Schulden mehr. Es zahlt jährlich eine konstante Annuität zurück.
Definition:
Unter der Annuität versteht man die jährliche Rück-Zahlung. Es ist die Summe aus Zinsen und Tilgung(srate).
|
| |
|
|
Modellierung
eines Tilgungsplanes
für den Fall, dass die Annuität konstant gehalten wird
|
|
Die Schulden (S) sind die betrachtete Größe. Die Tilgungsrate (Tr) wird jeweils zu Beginn eines Jahres von S_alt berechnet. Die Annuität ist eine Konstante (a). Die Zinsen (Z) berechnen sich bei einem Zinsfuß (p) immer auf den zum Jahresbeginn bestehenden Schuldenstand.
S = S_alt - Tr Anfangsgröße S = 15000000 €
Tr = a - Z und
Z = S_alt · p/100
bei p = 8 % und a = 1500000€
|
| |
|
|
Modellierung in einem Flussdiagramm |
|
 |
| |
|
|
| |
|
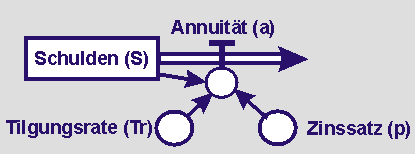
Die Schulden sind die Zustandsgröße und die Tilgungsrate ist die Flussgröße. Wir haben es in diesem Modell mit einem Abluss und nicht mit einer Zunahme zu tun.
S_neu < -- S_alt - Δt · Tr
Anfangsgröße S = 15000000 €
Δt = 1 (Zeittakt 1 Jahr)
Tr = a - (S · p/100)
a = 1500000 und p = 8 % |
| |
|
|
Programmierung in Excel |
|
Siehe hierzu:
ExcelDateien/Mappe7540a.htm (nur zur Ansicht) oder ExcelDateien/Mappe7540a.xls (herunterladbar und interaktiv) |
| |
|
|
Simulation
Das Simulationsergebnis entspricht der oben genannten Anfangsgröße und den oben angegebenen Parametern.
Simulationen mit anderen Anfangsgrößen und Parametern ergeben andere Ergebnisse.
|
|
 |
| |
|
|
Beschreibung des Veraltens,
des Zwecks und der Grenzen
des Modells |
|
Unter den gegebenen Bedingungen von 8% Zinsen und einer Annuität von 1500000€ sind die Schulden von 15000000€ in etwa 20 Jahren zurückgezahlt. (Würden keine Zinsen zu zahlen sein, dann wäre die Rückzahlung in 10 Jahren erfolgt, denn 10 · 1500000 = 15000000.) Bei kleinerem Zinssatz und höherer Annuität sind die Schulden in kürzerer Zeit zurückgezahlt.
Wie hoch müsste aber die jährliche Annuität bei einem Zinssatz von 8% und konstanter Tilgungsrate sein, wenn die Schulden in 10 Jahren abgezahlt sein sollten? Diese Frage führt an die Grenze dieses Modells. Eine Modellergänzung könnt wie folgt aussehen. |
| |
|
|
Modellergänzung
bei konstanter Tilgungsrate
Durch Simulation kann dann dann die Konstante Tr bestimmt werden, mit der nach 10 Jahren die Schulden abgetragen sind.
|
|
 |
| |
|
|
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
- Erstellt zur obigen Modellergänzung (oder Modellerweiterung) die Zustandsgleichung und weiteren Modellgleichungen.
- Programmiert das so beschriebene Modell in Excel.
- Findet durch Simulation die Tilgungsrate, die notwendig ist, um die Schulden nach 10 Jahren abzutragen.
- Experimentiert mit der Tilgung von Schulden den Kauf eines Mopeds auf Schuldenbasis.
- Hättet ihr beim Kauf eines Mopeds Bargeld zur Verfügung gehabt, wie viel hättet ihr sparen können?
|












