| |
|
|
| |
|
Wachstum im Weltmodell
oder Weltsystem
|
Berichte an den Club of Rome, |
|
|
1972, 1992 und 2004
Die Seitenangaben beziehen sich auf den Bericht aus dem Jahr 1972
|
|
„Jeder steht in ständiger Wechselwirkung mit allen anderen. Die Bevölkerung kann nicht wachsen ohne Ernährung; die Nahrungsmittelproduktion wächst mit der Zunahme des Kapitals; mehr Kapital erfordert mehr Rohstoffe; verbrauchte Rohstoffe tragen zur Umweltverschmutzung bei, und die Umweltverschmutzung beeinflusst wieder die Bevölkerungszunahme und das Ansteigen der Nahrungsmittelproduktion.“ (Die Grenzen des Wachstums, S 75) Literaturverweise: Dennis Meadows, Die Grenzen des Wachstums, Bericht an den Club of Rome zur Lage der Menschheit, dva, 1972.
Dieser Bericht und seine Folgeberichte "Die neuen Grenzen des Wachstums, 1992" und das "30Jahre-Update, 2004" enthalten eine Fülle an Zahlen, Grafiken und Interpretationen auch im Pro und Contra. |
| |
|
|
Aussagen der Berichterstatter
zum
Zweck des Weltmodells |
|
Im Modell sind nur die grundlegenden Beziehungen zwischen der Bevölkerung, der Nahrungsmittelversorgung, der Investition, den Abfallstoffen, Rohstoffen und der Produktion berücksichtigt ... bezogen auf die Weltbevölkerung als Ganzes. (Die Grenzen des Wachstums, S 82)
Die nationalen Grenzen auf der Erde bleiben unberücksichtigt. Die ungleiche Verteilung von Nahrungsmitteln, Rohstoffvorkommen und Kapital ist zwar in den Daten im Modell enthalten, ...
Formen der Bevölkerungsbewegung, klimatische Besonderheiten und politische Vorgänge werden nicht speziell berücksichtigt.
Welche Kenntnisse kann uns ein so vereinfachtes Modell vermitteln? Sind seine Aussagen sinnvoll? Im Sinn einer exakten Voraussage haben sie keinen Aussagewert. Wir können nicht die Bevölkerung der Vereinigten Staaten, das Nationalprodukt Brasiliens oder die Weltproduktion an Nahrungsmitteln im 2015 voraussagen. ....
Andererseits ist es außerordentlich wichtig, bessere Einsichten in die Ursachen für das Wachstum und für die Grenzen des Wachstums zu gewinnen und das Verhalten unseres sozialen und wirtschaftlichen Systems bei der Annäherung an Grenzgrößen zu durchschauen; .... (Die Grenzen des Wachstums, S 80) |
| |
|
|
Zentrale Schlussfolgerungen
des Berichtes von 1972 |
|
Wenn die gegenwärtige Zunahme der Weltbevölkerung, der Industrialisierung, der Umweltverschmutzung, der Nahrungsmittelproduktion und der Ausbeutung von natürlichen Rohstoffen unverändert anhält, werden die absoluten Wachstumsgrenzen auf der Erde im Laufe der nächsten hundert Jahre erreicht. (Wikipedia) |
| |
|
|
Zentrale Aussagen zu den
"neuen Grenzen des Wachstums" (1992) und des
"30-Jahre-Updates" (2004)
siehe Wikipedia |
|
Die neuen Grenzen des Wachstums wurden 1992 veröffentlicht. Neue Erkenntnisse (beispielsweise größere Rohstoffvorkommen als 20 Jahre zuvor bekannt) und die in der Zwischenzeit eingetretene Entwicklung wurden in die aktualisierten Simulationen aufgenommen, dennoch bleiben die Ergebnisse in der Tendenz ähnlich. Ebenso wie im 1972er Bericht enden die meisten Szenarien mit "Grenzüberziehung und Zusammenbruch".
Durch Geburtenbeschränkung, Produktionsbeschränkung, Technologien zur Emissionsbekämpfung, Erosionsverhütung und Ressourcenschonung ließe sich aber ein Gleichgewichtszustand erreichen. Je später mit diesen Maßnahmen begonnen würde, desto niedriger wäre der erreichbare materielle Lebensstandard. Insgesamt wurden 13 Szenarien in dem Bericht vorgestellt, von denen drei zu einem Gleichgewichtszustand führen.
Im Jahr 2004 veröffentlichten die Autoren das 30-Jahre-Update. Darin brachten sie die verwendeten Daten auf den neuesten Stand, nahmen leichte Veränderungen an ihrem Computermodell vor und errechneten anhand verschiedener Szenarien mögliche Entwicklungen ausgehend vom Jahr 2002 bis zum Jahr 2100. In den meisten der errechneten Szenarien ergibt sich ein Überschreiten der Wachstumsgrenzen und ein anschließender Kollaps bis spätestens 2100. Fortführung des „business as usual“ der letzten 30 Jahre führe zum Kollaps ab dem Jahr 2030.
Die Studie von 2004 geht auch auf die Entwicklung von 1972 bis 2002 ein. Sie beschreibt unter anderem eine Zunahme des sozialen Gefälles (20 % der Erdbevölkerung verfügten über 85 % des globalen BIP), eine Übernutzung des Bodens (40 % der Ackerflächen würden übernutzt), eine Überfischung (75 % der Fischbestände seien bereits abgefischt) und (wie bereits 1972) eine Erschöpfung fossiler Rohstoffe in wenigen Jahrzehnten. Die Autoren nehmen an, dass die Kapazität der Erde, Rohstoffe zur Verfügung zu stellen und Schadstoffe zu absorbieren bereits im Jahr 1980 überschritten worden sei und weiterhin überschritten werde (im Jahr 2004 schon um ca. 20 %).
|
|
|
|
| |
|
Wirkungsdiagramme und Modellbeschreibungen |
| |
|
zu "Bevölkerung, Kapital, Landwirtschaft und Umweltverschmutzung"
Die folgenden Seitenangaben beziehen sich auf den
Bericht an den Club of Rome aus dem Jahr 1972.
|
| |
|
|
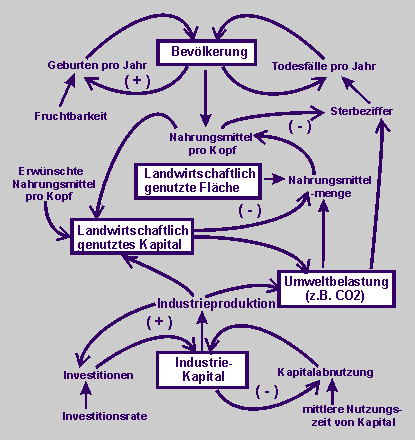
Wirkungsdiagramm der komplexen dynamischen Struktur von Bevölkerung, Kapital, Landwirtschaft und Umweltverschmutzung
(siehe: Seite 83) |
|
 |
| |
|
|
Beschreibungen zur komplexen dynamischen Struktur von Bevölkerung, Kapital, Landwirtschaft und Umweltverschmutzung |
|
Struktur von Regelkreisen: Ein Teil des durch Industriekapital entstehenden Produkts ist landwirtschaftliches Kapital (Traktoren, Bewässerungsanlagen und Düngemittel). Die Größen des landwirtschaftlichen Kapitals und der kultivierten Landfläche beeinflussen erheblich die Menge der erzeugten Nahrungsmittel.
Die Nahrungsmittelmenge pro Kopf hat wiederum starken Einfluss auf die Sterbeziffer. (S 84) ... Die industrielle wie die landwirtschaftliche Produktion können zur Umweltverschmutzung führen. ... (Und) die Umweltverschmutzung kann wiederum die Sterbeziffer direkt oder indirekt durch Senkung der landwirtschaftlichen Produktion beeinflussen. ....
Wenn alle Werte sonst konstant blieben, würde ein Bevölkerungszuwachs eine Abnahme der Nahrungsmittelmenge pro Kopf und dadurch eine höhere Sterblichkeit verursachen und über die steigende Zahl von Todesfällen allmählich wieder zu einer Abnahme der Bevölkerung führen. (S 84) ...
Wenn die Nahrungsmittelmenge pro Kopf unter das von der Bevölkerung verlangte Maß fällt, entsteht eine Tendenz, das landwirtschaftliche Kapital zu erhöhen, so dass die Nahrungsmittelerzeugung wieder gesteigert werden kann und zu einer Erhöhung der Nahrungsmittelmenge pro Kopf führt. (S 85)
Umweltverschmutzung: Praktisch jeder Schadstoff scheint exponentiell zuzunehmen. ... Einige Schadstoffe stehen in direktem Zusammenhang mit dem Bevölkerungswachstum oder der Wachstumsrate in der Landwirtschaft, die wiederum mit der Bevölkerungszunahme verknüpft ist. (S 59) |
| |
|
|
Betrachtung einer Teilstruktur:
Wirkungsdiagramm zur dynamischen Struktur des Wachstums der Weltbevölkerung
(siehe: Seite 26 ff) |
|
 |
| |
|
|
Flussdiagramm,
Zustands- und Modellgleichungen sowie Simulationen |
|
Flussdiagramm, Zustands- und Modellgleichungen sowie Simulationen sind analog zum Wachstum einer jeweden Population. Siehe aber die Hilfeseite "Bevölkerungswachstum". |
| |
|
|
Betrachtung einer Teilstruktur:
Wirkungsdiagramm zur dynamischen Struktur des Industrie-Wachstums
(siehe: Seite 26 ff)
|
|

|
| |
|
|
Beschreibungen zur
zur dynamischen Teil-Struktur
des Industriewachstums |
|
Mit einem bestimmten Grundstock an aktivem industriellem Kapital (wie Fabrikanlagen, Werkzeugmaschinen, Fahrzeugen) lässt sich jährlich eine bestimmte Menge an Industriegütern erzeugen. Wir gehen davon aus, dass Rohmaterial und Arbeitskraft in ausreichendem Maße vorhanden sind, dann beschränkt nur das Gesamtkapital die Produktionsmenge. ... Ein Teil der industriellen Jahresproduktion stellt aber selbst Industriekapital dar, wie Webstühle, Stahlwerke und Drehbänke, so genannte Industriegüter, die im Endeffekt das Industriekapital vergrößern. (S 30f)
Die Industriegüterproduktion bewirkt einen positiven Regelkreis: Größeres Kapital bewirkt eine höhere Produktion; ein Teil (Bruchteil) der Produktion wird zur Investition, und höhere Investition bedeutet mehr Kapital.
Das Kapital in Form von Investitionsgütern - nur in dieser Form ist Kapital produktionswirksam - nutzt sich ab und wird dann ausgeschieden, z.B. als Schrott. Deshalb gehört zu dem Modell auch ein negativer Regelkreis, der die Kapitalabnutzung berücksichtigt. Die jährliche Kapitalabnutzung wird umso größer, je höher die eingesetzte Kapitalmenge ist. (S 30f) |
| |
|
|
Übertragung des Wirkungsdiagramms zum Industriewachstum in ein Flussdiagramm |
|
 |
| |
|
|
Zustands- und Modellgleichungen zum Industriewachstum mit Quantifizierung der Modellgrößen |
|
K_neu <-- K_alt + Δt · (In - Ka)
Anfangsgröße Kapital K = 10 Billionen €; Δt = 1; ( 1 Zeittakt = 1 Jahr)
In = Ip · ir Λ Ip = K · b Λ Ka = K · f
ir = 0,2 Λ b = 0,4 Λ f = 0,02 |
| |
|
|
Programmierung in Excel
und Simulationen |
|
Siehe hierzu:
ExcelDateien/Mappe1229a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1229a.xls (herunterladbar und interaktiv) |
| |
|
|
Das Simulationsergebnis entspricht der Quantifizierung in den Modellgleichungen
Industriekapital blaue Rauten; Industrieproduktion lila Quadrate
|
|
 |
|
|
|
| |
|
Untersuchungen zur Teilstruktur
"Landwirtschaft und Kapital" |
| |
|
im komplexen Wirkungsgefüge von
Bevölkerung, Kapital, Landwirtschaft und Umweltverschmutzung |
| |
|
|
Erster Versuch
zur Untersuchung der Teilstruktur
"Landwirtschaft und Kapital"
(violett unterlegt)
im komplexen Wirkungsgefüge
von Bevölkerung, Kapital, Landwirtschaft und Umweltverschmutzung
(siehe: Seite 83) |
|
 |
| |
|
|
Beschreibungen zur
zur dynamischen Teil-Struktur
"Landwirtschaft und Kapital" |
|
Wenn die Nahrungsmittelmenge pro Kopf unter das von der Bevölkerung verlangte Maß fällt, entsteht eine Tendenz, das landwirtschaftliche Kapital zu erhöhen, so dass die Nahrungsmittelerzeugung wieder gesteigert werden kann und zu einer Erhöhung der Nahrungsmittelmenge pro Kopf führt. (S 85).
Wichtigste Grundlage für die Nahrungsmittelproduktion ist bebaubares Land. Nach neueren Untersuchungsergebnissen gibt es auf der Erde etwa 3,2 Milliarden Hektar prinzipiell landwirtschaftlich nutzbare Flächen. Die Hälfte davon, und zwar die ertragreichere, leicht bebaubare Hälfte, wird bereits landwirtschaftlich genutzt. Für die andere Hälfte sind hohe Kapitalsummen für Bewässerung, Rodung, Düngung und ähnliche Maßnahmen der Urbarmachung erforderlich, wenn man sie ebenfalls nutzen will. Die Durchschnittskosten in unbesiedelten Gebieten belaufen sich auf etwa 1150 Dollar pro Hektar (ha) .... (S39) ...
Jeder Mensch benötigt bei der gegenwärtigen Produktionsrate etwa 0,4 ha zu seiner Ernährung. (S 40)
|
| |
|
|
Erster Versuch
einer Übertragung der violett unterlegten Teilstruktur in ein mögliches Flussdiagramm unter Beachtung der Beschreibungen
Entscheidende Fragen bei der Übertragen sind:
Welche Größen sind Zustands- oder Flussgrößen? Wo sind "Anpassungsfaktoren" einzubauen, damit die Dimension wieder stimmt? Kann etwa die
landwirtschaftlich genutzte Fläche auch als eine Zustandsgröße betrachtet werden? ...
|
|
 |
| |
|
|
| Zustands- und Modellgleichungen zurTeilstruktur
"Landwirtschaft und Kapital"
mit einer Quantifizierung der Modellgrößen !
Doch woher kommen die Größen? b2, b3, f2 und f3 sind experimentelle Größen, "enk" ist eine Wunschgröße an Energie, die alle Menschen erhalten sollen, "bz" ist die Bevölkerungszahl und "F" die zur Zeit genutzte landwirtschaftlich Fläche. |
|
K_neu <-- K_alt + Δt · (In - Ka) (siehe oben)
Anfangsgröße Kapital K = 10 Billionen €;
Δt = 0,1; ( 1 Zeittakt = 1 Jahr)
LK_neu <-- LK_alt + Δt · (Z_LK - Z_NP)
Anfangsgröße landwirtschaftlich genutztes Kapital LK = 3 Billionen €;
Δt = 0,1; ( 1 Zeittakt = 1 Jahr)
NP_neu <-- NP_alt + Δt · Z_NP
Anfangsgröße Nahrungsproduktionsmenge NP = 20 Bill. Tonnen;
Δt = 0,1; ( 1 Zeittakt = 1 Jahr)
In = Ip · ir Λ Ip = K · b1 Λ Ka = K · f1 (siehe oben)
Z_LK = (enk - nk) · Ip · b2 · f3 Λ
nk = NP / bz Λ Z_NP = LK · F · f2
ir = 0,2 Λ b1 = 0,4 Λ f1 = 0,02
ir = 0,2 Λ b1 = 0,4 Λ f1 = 0,02 Λ enk = 3,1 Λ b2 = 0,4 Λ
F = 2,7 Λ f2 = 0,4 Λ f3 = 2,9 Λ bz = 6,8
|
| |
|
|
Programmierung in Excel
und Simulationen |
|
Siehe hierzu:
ExcelDateien/Mappe1229b.htm (nur zur Ansicht) oder ExcelDateien/Mappe1229b.xls (herunterladbar und interaktiv)
|
| |
|
|
Kommentar zur Interpretation |
|
Das Modell ist zwar mathematisch aber nicht inhaltlich interpretierbar. Die Gründe dafür sollten selbst gefunden werden!
Konsequenzen:
- Es ist zunächst eine weitere Vereinfachung sinnvoll, ehe sie in ein komplexeres Modell eingebunden wird.
- Die" landwirtschaftlich genutzte Fläche" muss ebenfalls als Zustandsgröße betrachtet werden.
- Und: "Landwirtschaftlich genutztes Kapitel" und "Nahrunsproduktion" hängen zwar voneinander ab, können aber nicht in Reihe "geschaltet" werden.
- Und: Für die landwirtschaftlich genutzte Fläche muss eine Wachstumsrate überlegt werden, aber wie?
|
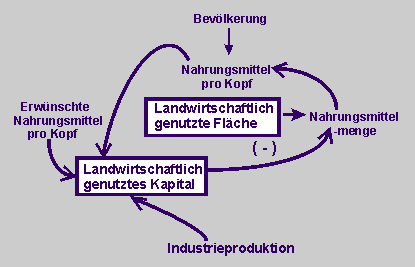
Zweiter Versuch
zur Untersuchung der Teilstruktur
"Landwirtschaft und Kapital"
in einem einfacheren Wirkungsgefüge
|
|
 |
| |
|
|
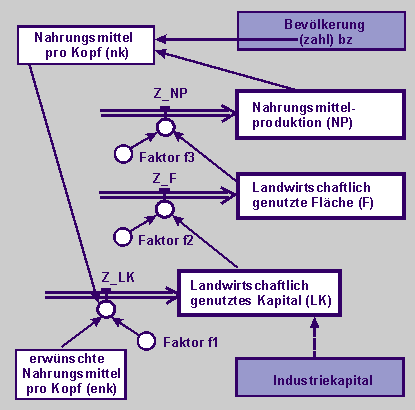
Zweiter Versuch
einer möglichen Übertragung
der Teilstruktur
"Landwirtschaft und Kapital"
in ein Flussdiagramm
(Anmerkung:
Die violett unterlegten Größen sind zwei An- bzw. Einbindungsknoten in der komplexen Struktur)
|
|
 |
| |
|
|
Zustands- und Modellgleichungen zurTeilstruktur
"Landwirtschaft und Kapital"
mit einer Quantifizierung der Modellgrößen |
|
LK_neu <-- LK_alt + Δt · Z_LK
Anfangsgröße landwirtschaftlich genutztes Kapital LK = 4 Billionen €;
Δt = 0,3; ( 1 Zeittakt = 1 Jahr)
F_neu <-- F_alt + Δt · Z_F
Anfangsgröße landwirtschaftlich genutzte Fläche F = 1,5 Mill. ha;
Δt = 0,3; ( 1 Zeittakt = 1 Jahr)
NP_neu <-- NP_alt + Δt · Z_NP
Anfangsgröße Nahrungsproduktionsmenge NP = 10 Bill. Tonnen;
Δt = 0,3; ( 1 Zeittakt = 1 Jahr)
Z_LK = (enk - nk) · f1 Λ F = LK · f2 Λ
Z_NP = F · f3 Λ nk = NP/ bz
enk = 3,1 Λ f1 = 0,2 Λ f2 = 0,01 Λ f3 = 0,4 Λ bz = 6,8
|
| |
|
|
Programmierung in Excel
und Simulationen |
|
Siehe hierzu:
ExcelDateien/Mappe1229c.htm (nur zur Ansicht) oder ExcelDateien/Mappe1229c.xls (herunterladbar und interaktiv) |
|
|
|
| |
|
Wirkungsdiagramme und Modellbeschreibungen |
| |
|
zu "Bevölkerung, Kapital, Dienstleistungen und Rohstoffen"
Die folgenden Seitenangaben beziehen sich auf den
Bericht an den Club of Rome aus dem Jahr 1972.
|
| |
|
|
Detail-Beschreibungen einer anderen komplexen dynamischen Struktur von Bevölkerung, Kapital, Dienstleistungen und Rohstoffen (siehe: Seite 85 f) |
|
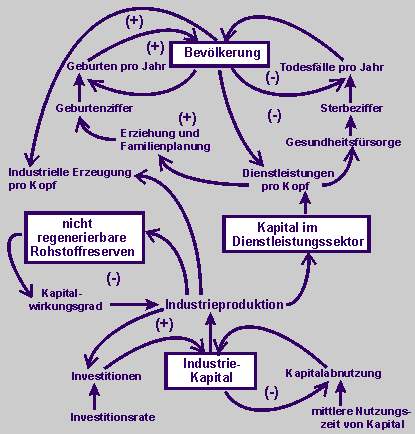
Ein Teil des Industrieproduktes sind Güter, die zum Dienstleistungskapital gehören wie Schulen, Krankenhäuser, Banken und die zugehörigen Einrichtungen. Der Nutzen dieses Dienstleistungskapitals, geteilt durch die Bevölkerungszahl, ergibt den durchschnittlichen Wert der Dienstleistungen pro Kopf, der wiederum den Stand des Gesundheitswesens und damit die Sterblichkeit beeinflusst. Zu den Dienstleistungen gehören auch Erziehungswesen und Forschungsarbeiten zur Geburtenkontrolle ebenso wie die Förderung von Geburtenkontrollemaßnahmen durch Informationsschriften und schliche Hilfsmittel. Die Dienstleistungen pro Kopf beeinflussen so auch die Fruchtbarkeit.
Auch eine Änderung des Industrieproduktes pro Kopf hat zeitlich stark verzögert über soziale Faktoren Einfluss auf die Fruchtbarkeit.
Jede Einheit industrieller Produktion benötigt eine bestimmte Menge nicht regenerierbarer Rohstoffe. Mit der langsamen Erschöpfung der Rohstoffvorräte wird immer mehr Kapital erforderlich, um gleiche Mengen von Rohstoffen zu gewinnen. Damit sinkt die Wirksamkeit des Kapitals. (S 85) |
| |
|
|
Wirkungsdiagramm der komplexeren dynamischen Struktur von Bevölkerung, Kapital, Dienstleistungen und Rohstoffen
(siehe: Seite 86f) |
|
 |
| |
|
|
Das gesamte Weltmodell enthält insgesamt 99 Größen: Zustandsgrößen, Flussgrößen, Parameter und messbare Größen
Es wird hier nicht dargestellt.
|
|
Die Wechselwirkungen in den beiden zuvor dargestellten Wirkungsdiagrammen sind typisch für viele miteinander verkettete Regelkreise innerhalb des Weltmodells. Andere Regelkreise erfassen Faktoren wie die Fläche kultivierten Landes auf der Erde und die Raten seiner Urbarmachung und Erosion, die Daten für die Freisetzung von Schadstoffen und deren Abbau in der Umwelt, und den Gleichgewichtszustand zwischen verfügbarer Arbeitskraft und der Zahl der vorhandenen Arbeitsplätze. (S 88 ff) |
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
- Stellt selbst ausgewählte Teildynamiken aus den obigen Wirkungsdiagrammen in Flussdiagrammen dar, programmiert und simuliert sie. Zum Beispiel:
- Bringt die Dynamik von Bevölkerung, Kapital und Landwirtschaft in einem Flussdiagramm zusammen, programmiert und simuliert sie.
- Stellt die Dynamik von Kapital und Umweltbelastung in einem Wirkungs- und Flussdiagramm dar. Programmiert und simuliert die Dynamik.
- Stellt die Dynamik von Bevölkerung, Dienstleistung, Familienplanung und Gesundheitsfürsorge in einem Flussdiagramm dar, programmiert und simuliert sie.
|












