|
|
|
Der Arbeitsbereich "Modellierung und Simulation dynamischer Systeme" liegt ab 2008 auf dem Bildungsserver von Herrn Kohorst (in Lemgo) seitdem learn-line, der ehemalige Bildungsserver in NRW, abgeschaltet worden ist. |
| |
|
|
|
Mögliche neue Schlüsselqualifikationen oder Kompetenzen:
Komplexität und Dynamik verstehen lernen
|
|
Dynamische Systeme zu modellieren und zu simulieren ist für Lehrende wie für Lernende ein neues aber wichtiges Gebiet. Denn mit der Behandlung von Komplexitäten insbesondere von dynamischen Systemen verbinden sich zukunftorientierte, wichtige neue Bildungsziele.
An alle, die mit der Modellierung und Simulation dynamischer Systeme im Unterricht experimentieren, stellt sich also die Frage: Wo und in welchen unterrichtlichen Zusammenhängen können mit Hilfe der Methode der "system dynamics" Erkenntnisse gewonnen werden, die auf konventionelle Art nicht oder nur schwer zu gewinnen sind? Antworten auf diese Frage sollen im Arbeitsbereich gesammelt werden.
|
| |
|
|
|
Grundlegende Informationen zur Systemdynamik
|
|
Auch Lehrende müssen sich also in der Regel zunächst mit der grundlegenden Theorie zur Systemdynamik vertraut machen. Hierzu werden im Arbeitsbereich die folgenden grundlegenden Informationen angeboten:
|
|
Überblick über die Inhalte
der Mediothek des Arbeitsbereiches
|
|
In der Mediothek des Arbeitsbereiches befinden sich Literaturhinweise, kommentierte Links ins WWW, ausführlich dokumentierte Unterrichtsreihen sowie eine Sammlung von Modellen aus unterschiedlichen Fächern.
Sowohl die Modelle als auch die Unterrichtsbeispiele lassen sich aus der "Liste der Eingangsseiten" einzeln als htm-Seiten herunterladen und vor Ort an die konkreten Anforderungen anpassen. Ebenso kann aber auch der gesamte Arbeitsbereich auf den eigenen Rechner gespeichert werden.
Bei der Modell-Bildung und Modell-Simulation wird immer das Werkzeug Dynasis genutzt. |
| |
|
|
|
In der Mediothek angebotene Unterrichtsprojekte oder Unterrichtsreihen
|
|
In der Mediothek werden die folgenden Unterrichtsprojekte oder Unterrichtsreihen angeboten. Auch sie können als htm-Seiten einzeln heruntergeladen werden.
|
|
In der Mediothek aufbereitete und angebotene dynamische Systeme mit zugehörigen Dynasis-Modellen
|
|
Bei den insgesamt 16 dynamischen Systemen aus Biologie, Chemie, Physik, Geografie und Medizin, die in der Mediothek aufbereitet sind und angeboten werden, spielt immer und unvermeidlich auch die "Mathematik" eine zentrale Rolle. Alle System-Beispiele eignen sich also mehr oder weniger als "reale Probleme", wie sie in dieser Arbeitsumgebung "Modellieren mit Mathe" vorgeschlagen werden. Sie könnten also in einer Modellierungsphase behandelt werden. Einige Beispiele werden daher unten als Nutzungmöglichkeiten dieser Arbeitsumgebung skizziert und dann mit der jeweiligen Eingangsseite auf learn-line verlinkt.
|
|
|
|
|
| |
|
|
|
Angebote in der Mediothek für die Systematisierungsphase
|
|
Für die Systematisierungphase - die auf jede Modellierungsphase folgen sollte - bieten sich als Hilfen auch die folgenden Angebote aus der Mediothek an:
Modelltypen (für 9te Klassen und höher):
Rechenverfahren (für 11te Klassen und höher):
|
|
|
|
| |
|
Beispiele zur Modellierung und Simulation dynamischer Systeme
|
| |
|

|
| |
|
Achtung: Die Links in den
folgenden Beispielen führen zu den Eingangsseiten der Modelle im Arbeitsbereich
"Modellierung und Simulation dynamischer Systeme". Von diesen
Eingangsseiten aus werden immer die folgenden weiterführenden Informationen
angeboten: die Differenzengleichungen des Systems, die Grafen einer Simulation
und unterrichtliche Anregungen, häufig sogar ausführliche Anregungen! |
|
|
|
|
Algenblüte
Jede Population zeigt in einem unbegrenzten Lebensraum ein exponentielles Wachstum, d.h: in konstanten Zeiträumen verdoppelt sich die Populationsgröße. Da es aber immer Begrenzungen gibt, ist das exponentielle Wachstum nur eine zeitweilige Erscheinung.
|
|
Exponentielles und logistisches Wachstum
Beide Modelle enthalten jeweils nur eine Zustandsgröße.
|
| |
|
|
|
Algenwachstum
abhängig von Nährsalzen
Algen benötigen zum Wachstum Ressourcen und diese regeln ihr Wachstum.
Algen nehmen Nährsalze auf, geben aber beim Absterben auch wieder - über hier nicht dargestellte Prozesse - Nährsalze zurück. Dabei wird hypothetisch davon ausgegangen worden, dass jeweils 10% der Algen absterben.
|
|
Ressourcenorientiertes Wachstum: Grundmodell
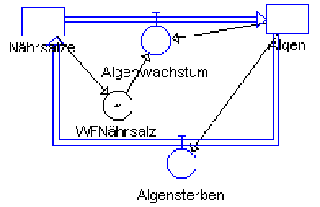
Im Modell hängen zwei Zustandsgrößen voneinander ab.
|
| |
|
|
|
Selbstreinigung
von Gewässern
Mit Hilfe des nebenstehenden Modells kann die kurzfristige Einleitung organischer Abfallstoffe, ihre dauernde Einleitung und ihre dauernde und überhöhte Einleitung simuliert werden. Bei diesem Modell steht also die Simulation im Vordergrund und nicht die Modellierung selbst. Dazu werden zusätzliche unterrichtliche Anregungen gegeben und Antworten auf häufig gestellte Fragen gegeben.
|
|
Ressourcenorientiertes Wachstum am Beispiel der Selbstreinigung eines Gewässers

Im Modell hängen drei Zustandsgößen voneinander ab.
|
| |
|
|
|
Harnweg-Infektion
In der Regel verhindern die körpereigenen Abwehrkräfte ein Überhandnehmen der bakteriellen Belastung. Werden diese Abwehrkräfte aber geschwächt, können sich die Bakterien rasant vermehren und führen zu einem typischen Beschwerdebild. Eine Behandlung, hier mit bakterizid wirkenden Antibiotika, ergänzt die geschwächten Abwehrkräfte und trägt mit zum Rückgang und zum Verschwinden der Infektion bei, so lange die Behandlung ausreichend lange und mit ausreichend hoher Dosis durchgeführt wird.
|
|
Der dynamische Verlauf einer Harnweg-Infektion
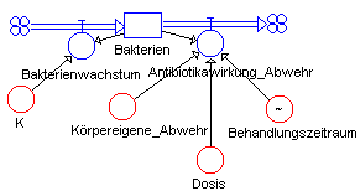
In diesem Modell gibt es nur eine Zustandsgröße: die Bakterien.
|
| |
|
|
|
Grippen-Epidemie
Bei einer Epidemie ist ein wichtiger Gesichtspunkt das regelmäßige Aufflackern während des Verlaufs der Epidemie, bei der in Wellen ganze Gruppen einer Bevölkerung betroffen sein können.
Die Ursachen für diesen wellenförmigen Verlauf können vielfältig sein. Das hier gewählte Modell beschränkt die Erklärung auf die Faktoren Erkankungs- und Immunitätsdauer sowie Infektiösität der Infektion.
|
|
Der dynamische Verlauf einer Epidemie
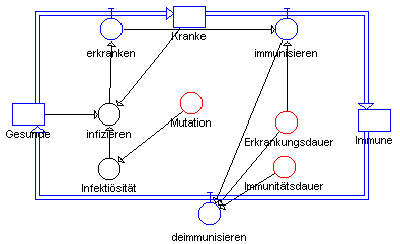
In diesem Modell spielen drei Zustandsgrößen eine Rolle.
|
|
|
|
|
Bevölkerungsmodell
Das hier vorgestellte Modell zeigt das einfachste Modell einer Bevökerungsentwicklung. Es arbeitet mit den elementaren Angaben Bevölkerungszahl, Geburtenziffer und Sterbeziffer und abstrahiert von der Geschlechts- und Altersdifferenzierung.
|
|
Bevölkerungsmodell: Natürlich wachsende Bevölkerung

|
| |
|
|












