|
|
Parallelogramme, Rechtecke und Quadrate
|

|
|

|
|

|
|

|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
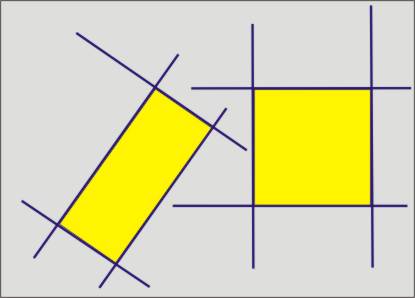
Ein Parallelen-Paar sind zwei Geraden,
die parallel verlaufen.
Zwei Parallelen-Paare
können sich schneiden und dabei sogar senkrecht
aufeinander stehen. Dabei
entstehen immer Parallelogramme!
|
|
 |
| |
|
|
Stehen zwei Parallelen-Paare senkrecht
aufeinander, so entstehen Rechtecke.
Sind zusätzlich die vier Seiten
des Rechtecks gleich lang, so entstehen Quadrate.
|
|
 |
| |
|
|
|
|
|
|
| |
|
|
|
Ideen für mögliche,
selbstorganisierte
Übungen:
|
|
- Alle Quadrate sind Rechtecke. Alle Rechtecke
sind Parallelogramme. Argumentiert in eurer
Gruppe, warum das so ist.
- Besprecht miteinander, ob auch die umgekehrten
Aussagen gültig sind: Sind alle Rechtecke
Quadrate? Sind alle Parallelogramme Rechtecke?
- Besprecht miteinander, wie sich eine Behauptung
widerlegen lässt.
- Zeichnet mit dem Geodreieck Parallelogramme,
Rechtecke und Quadrate.
- Gestaltet ein Bild mit vielen gleichen Parallelogrammen.
|
|
|
|
|
Eine Parallelkonstruktion
oder eine Konstruktion aus Rechtecken und Quadraten.
|
|
 |
| |
|
|
|
|
|
 |
| |
|
Victor Vasarely, Heckla-Violet,
1969
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
© Pädagogisches
Institut für die deutsche Sprachgruppe Bozen 2000 -
. Letzte Änderung:
23.11.2015
|
 |
|
|
|














