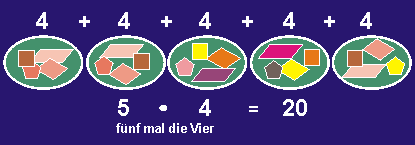|
|
|
|
|
|
|
Die Multiplikation
der natürlichen Zahlen wird
an einem Beispiel erklärt:
|
|
|
| |
|
|
|
|
|
Jede der grünen Mengen
hat 4 Elemente, also die Mächtigkeit 4.
Im Beispiel haben wir 5 Mengen mit der Mächtigkeit
4.
Also gibt es 5 mal 4 Elemente.
Insgesamt sind es 20 Elemente.
Die Zahl 20 ist das Produkt von 5 und
4.
Die beiden Zahlen 5 und 4 heißen
Faktoren.
5 mal 4 gleich 20
5 · 4 = 20
|
| |
|
|
|
|
|
| |
|
|
|
Die Multiplikation
von natürlichen Zahlen kann immer auf die
Addition zurückgeführt werden.
|
|
6 ·
3 = 3 + 3 + 3 + 3 + 3 + 3 = 18
7 ·
5 = 5 + 5 + 5 + 5 + 5 + 5 + 5 = 35
8 ·
9 = 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 72
3 ·
6 = 6 + 6 + 6 = 18
|
| |
|
|
|
|
|
| |
|
|
|
Die Division
der natürlichen Zahlen wird
an einem Beispiel erklärt
und auf die Multiplikation zurückgeführt:
Den Sternenhimmel mit
20 Sternen könnt ihr aufteilen in 4 Mengen
mit der Mächtigkeit 5.
|
|
 |
| |
|
Die Zahl 5 muss mit 4 multipliziert
werden, damit 20 herauskommt.
4 ist der Quotient von 20 und 5. |
| |
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|
|
|
|
| |
|
|
|
Ideen für mögliche
selbstorganisierte
Übungen:
|
|
Das "Kleine Einmaleins"
- Schreibt die Produkte 5·7
und 6·5 und 7·7
und 9·8 jeweils als
Summe.
- Wählt selbstständig weitere Produkte
und schreibt sie als Summe.
- Erweitert die folgende Tabelle auf eine 10
mal 10 Tabelle und füllt sie zu Ende aus.
- Füllt ebenso die dann folgende Multiplikationstafel
für das "Kleine Einmaleins" zu
Ende aus.
|
| |
|
|
1·1 = 1
|
2·1 = 2
|
3·1 = 3
|
...
|
10·1 =
10
|
|
1·2 = 2
|
2·2 = 4
|
3·2 = 6
|
...
|
10·2 =
20
|
|
1·3 = 3
|
2·3 = 6
|
3·3 = 9
|
...
|
10·3 =
30
|
|
1·4 = 4
|
2·4 = 8
|
3·4 =12
|
...
|
10·4 =
40
|
|
....
|
....
|
....
|
...
|
....
|
|
1·10 =10
|
2·10 =20
|
3·10 =30
|
...
|
10·10 =100
|
|
| |
|
|
| |
|
|
·
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
|
|
3
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
8
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
30
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
|
|
72
|
|
|
9
|
|
|
|
|
|
|
|
|
|
|
|
10
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| |
|
- Übt das "Kleine Einmaleins"
und lernt es auswendig.
|
| |
|
|
|
|
|
| |
|
|
|
|
Anmerkungen zum Auswendiglernen
des "Kleinen Einmaleins"
Eigentlich braucht ihr keine 100 Sätze
zu lernen, sondern nur 55 :
Wenn ihr wisst, was 2·3
ist, dann wisst ihr auch, was 3·2
ist.
- Als Test, ob ihr das "Kleine Einmaleins"
gut könnt, solltet ihr ganz schnell sagen
können:
- Mit welcher Zahl muss die 4
multipliziert werden, um 20
zu erhalten?
- Mit welcher Zahl muss die 8
multipliziert werden, um 40
zu erhalten?
- Mit welcher Zahl muss die 10
multipliziert werden, um 80
zu erhalten?
...
- Stellt euch in eurer Kleingruppe weitere Aufgaben
dieser Art.
|
|
|
|