blikk
logo
kidszone punkt
infothek forum galerie sitemap

Zweistellige Zahl mal zweistellige Zahl - Wie geht das?

anfang zurück weiter ans ende eine ebene nach oben

Das Verfahren (der Algorithmus) der schriftlichen Multiplikation natürlicher Zahlen wird in der Folge an Beispielen eingeführt und begründet.
  

   

Das Verfahren wird
zunächst an einem Beispiel
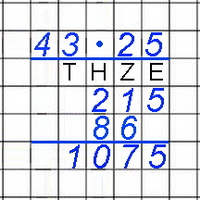
in zwei unterschiedlichen Schreibweisen vorgestellt:

rechne 5 · 3 = 15
schreibe 5 unter die Einer
merke 1 (Zehner)

rechne 5 · 40 = 200
schreibe 20 + 1, also 21 unter die Zehner und Hunderter

rechne 20 · 3 = 60
schreibe 6 unter die Zehner

rechne 20 · 40 = 800
schreibe 8 unter die Hunderter

Dann addiere 215 + 860

  

 

 

 

 

 

 

 

  


Begründung
des Verfahrens
  (40 + 3 ) · (20 + 5)
=(40·20)+(40·5)+(3·20)+(3·5)

  (40·20)+(40·5)+(3·20)+(3·5) =(3·5)+(40·5)+(3·20)+(40·20)

 (3·5)+(40·5)+(3·20)+(40·20)
=15 + 200 + 60 + 800
=215 + 860 = 1075
 
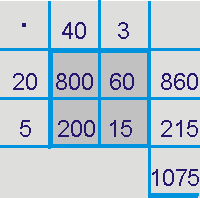
Die Rechnung im Malkreuz
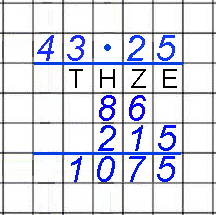
Bei der zweiten Schreibweise werden die Multiplikationen umgekehrt durchgeführt.

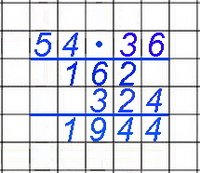
Bei zwei weiteren Beispielen wird nur noch die zweite Schreibweise in verkürzter Form verwendet.

rechne 3· 4 = 12
schreibe 2 unter die Zehner
merke 1 (Hunderter)

rechne 3· 5 = 15
schreibe 15 +1, also 16,
die 6 unter die Hunderter und die 1 unter die Tausender

rechne 6 · 4 = 24
schreibe 4 unter die Einer
und merke 2 (Zehner)

rechne 6 · 5 = 30
schreibe 30 + 2, also 32 unter die Zehner und Hunderter
Dann addiere.

 

  

Die Rechnungen in verkürzter Form

 

 

 

 

 

 

 

 

  

  Begründung
des Verfahrens
(50 + 4 ) · (30 + 6)
=(50·30)+(50·6)+(4·30)+(4·6)
  (50·30)+(50·6)+(4·30)+(4·6)
=(50·30)+(4·30)+(50·6)+(4·6)
 (50·30)+(4·30)+(50·6)+(4·6)
=1500 + 120 + 300 + 24
=1620 + 324 = 1944

 

 

 
Die Rechnung im Malkreuz
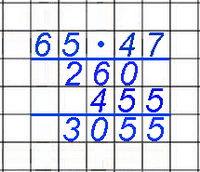
Die Einleitungsaufgabe oben im Malkreuz
    
Einführungen und Fortsetzung der schriftlichen Rechenverfahren:
 
 
 
     

Ideen für mögliche, selbstorganisierte
Übungen:

 

Nutzt die Druckexemplare:


 

 

  
  • Erläutert in eurer Kleingruppe, wie ihr bei der letzten Multiplikation oben rechnen könnt.
  • Argumentiert an diesem Beispiel aber auch, warum ihr so rechnen dürft.

Gebt euch in eurer Kleingruppe gegenseitig schriftliche Multiplikationsaufgaben vor, wobei zweistellige Zahlen mit zweistelligen multipliziert werden sollen.

  • Führt das schriftliche Rechenverfahren jeweils in der zweiten Schreibweise aus.
  • Rechnet jeweils alle Multiplikationen auch im Malkreuz und mit Malstreifen.
  • Überprüft euch gegenseitig, indem ihr euch den Rechenverlauf vorsagt. Nutzt bei der Überprüfung eures Ergebnisses aber auch den Taschenrechner.
zum seitenanfang