|
|
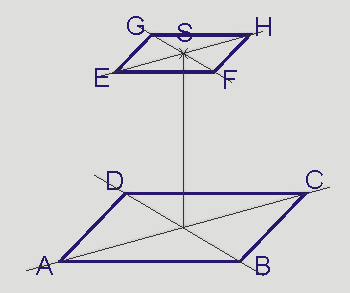
Ein Schrägbild eines Pyramidenstumpfes
|

|
|

|
|

|
|

|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Die Glasbauten von Biosphere II in Arizona sind
regelmäßige Pyramidenstümpfe
auf quadratischen Grundflächen.
|
|
 |
| |
|
|
| |
|
Und so könnt ihr das Schrägbild
eines regelmäßigen Pyramidenstumpfes
mit quadratischer Grund- und Deckfläche zeichnen
oder konstruieren: |
| |
|
|
Schritt 1: Die quadratische
Grundfläche der Pyramide (linke Figur)
wird als Parallelogramm ABCD (rechte Figur)
gezeichnet. Die nach hinten verlaufenden Kanten
werden im Winkel von 45° gezeichnet und
in ihrer Länge halbiert.
|
|
 |
|
| |
|
|
|
|
Schritt 2: Die
quadratische Deckfläche EFGH, deren Seitenkanten
nur halb so lang sind wie die Grundkanten, wird
in derselben Weise gezeichnet oder konstruiert.
|
|
 |
|
| |
|
|
|
|
Schritt 3: Der
Mittelpunkt S der quadratischen Deckfläche
EFGH, liegt senkrecht über dem Mittelpunkt
M der Grundfläche ABCD.
Die Höhe des Stumpfes wird
in dieser Figur beliebig lang angenommen.
|
|
|
|
| |
|
|
|
|
Schritt 4: Die
Eckpunkte E, F, G und H der Deckfläche werden
mit den Eckpunkten A, B, C und D der Grundfläche
verbunden.
Sichtbare Linien werden durchgezeichnet. Nicht
sichtbare Linien werden punktiert.
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
Ideen für mögliche,
selbstorganisierte
Übungen:
|
|
- Konstruiert - wie oben beschrieben - das Schrägbild
eines Pyramidenstumpfes, der als Grund- und
Deckfläche ein gleichseitiges Dreieck besitzt.
Beachtet: Die Seitenlänge des Dreiecks
der Deckfläche soll nur halb so lang sein
wie die der Grundfläche.
- Konstruiert ein Schrägbild eines unregelmäßigen
(beliebigen) Pyramidenstumpfes.
- Lassen sich auch andere Arten von Schrägbildern
erzeugen?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
© Pädagogisches
Institut für die deutsche Sprachgruppe Bozen 2000 -
. Letzte Änderung:
22.05.2013
|
 |
|
|
|