Mit einem Geodreieck g an s spiegeln

Erster Schritt:

Gegeben sind eine Originalgerade g und eine Spiegel-
gerade s. Auf der Originalgeraden g werden zwei beliebige Punkte P und Q eingetragen.
Zur Erinnerung: Eine Gerade ist durch zwei Punkte eindeutig bestimmt.

Zweiter Schritt:

Der Originalpunkt P wird
an s gespiegelt. Es entsteht der Bildpunkt P'.

Mit einem Geodreieck P an s spiegeln

Dritter Schritt:

Der Originalpunkt Q wird
an s gespiegelt. Es entsteht der Bildpunkt Q'.

Vierter Schritt:

Die Gerade durch P' und Q' ist die Bildgerade g'.

Ideen für mögliche, selbstorganisierte
Übungen:

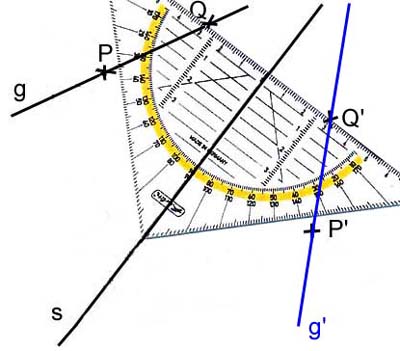
Überlegt euch, welche möglichen Fehler bei der Konstruktion auftreten können.
Gebt euch ein beliebiges Dreieck ABC und eine Spiegelachse s außerhalb des Dreiecks vor. Spiegelt das Dreieck an s. Messt die Seitenlängen im Orginaldreieck und im Bilddreick. Was fällt euch auf?
Gebt euch ein rechtwinkliges Dreieck ABC und eine Spiegelachse s außerhalb des Dreiecks vor. Spiegelt das Dreieck an s. Messt die Innenwinkel im Originaldreieck und im Bilddreieck. Was fällt euch auf?

Konstruktion einer Dreifachspiegelung an parallelen Geraden

Konstruktion einer mosaikartigen Achsensymmetrie