|
Die Vorschrift zum Ausfüllen der Multiplikationstafel
wird durch vier Beispiele erläutert:
1·3 = 3
(hellgrünes Feld)
4·2 = 8
(blaues Feld)
5·6 = 30
(orangenes Feld)
8·9 = 72
(dunkelgrünes Feld)
|
|
|
·
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
|
|
3
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
8
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
30
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
|
|
72
|
|
|
9
|
|
|
|
|
|
|
|
|
|
|
|
10
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| |
|
Der erste Faktor ist immer aus der linken
Spalte, der zweite immer aus der ersten Zeile. |
| |
|
|
|
|
|
|
| |
|
|
|
Ideen für mögliche,
selbstorganisierte
Übungen:
|
|
- Füllt die Tafel vollständig aus,
ohne von der folgenden Tafel abzuschreiben!
- Betrachtet dann aber die vollständig
ausgefüllte Multiplikationstafel für
das "Kleine Einmaleins" und fragt
euch:
- Gibt es wie bei der Addition auch in der Multiplikationstafel
eine Symmetrieachse?
- Welche Bedeutung hat diese Symmetrie?
- Was fällt euch sonst noch alles an dieser
Tafel auf?
|
| |
|
|
| |
|
|
·
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
2
|
2
|
4
|
6
|
8
|
10
|
12
|
14
|
16
|
18
|
20
|
|
3
|
3
|
6
|
9
|
12
|
15
|
18
|
21
|
24
|
27
|
30
|
|
4
|
4
|
8
|
12
|
16
|
|
|
|
|
|
|
|
5
|
5
|
10
|
15
|
|
25
|
30
|
|
|
|
|
|
6
|
6
|
12
|
18
|
|
|
36
|
|
|
|
|
|
7
|
7
|
14
|
21
|
|
|
|
49
|
|
|
|
|
8
|
8
|
16
|
24
|
|
|
|
|
64
|
72
|
|
|
9
|
9
|
18
|
27
|
|
|
|
|
|
81
|
|
|
10
|
10
|
20
|
30
|
|
|
|
|
|
|
100
|
|
| |
|
|
|
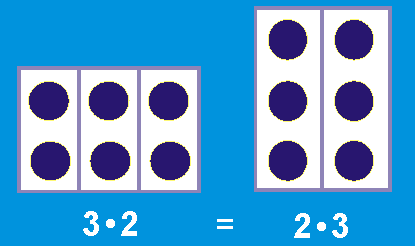
Veranschaulichung
der Vertauschbarkeit
der beiden Faktoren
an einem Beispiel:
|
|
 |











