|
|
|
|
|
|
|
|
|
|
|
Zuordnungsvorschrift, Funktionsterm, Funktionsgleichung und Lösung
einer Funktion
|
|

|

|

|

|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vorschriften oder
Regeln
|
|
Beispiel 1
|
|
Beispiel 2
|
|
für Zuordnungen
|
|
|
|
|
|
|
|
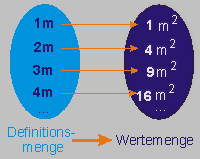
Quadriere die Größe
aus der Definitionsmenge, dann erhälst du
die zugeordnete Größe aus der Wertemenge.
|
|
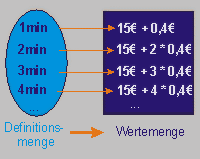
Multipliziere die
Maßzahl aus der Definitionsmenge mit 0,40€
und addiere 15 €, dann erhälst du die
zugeordnete Größe aus der Wertemenge.
|
| |
|
|
|
|
| |
|
 |
|
 |
| |
|
|
|
|
| |
|
Diese Vorschrift lässt
sich auch inhaltlich deuten: Den Längen eines
Quadrates wird sein Flächeninhalt zugeordnet.
|
|
Diese Vorschrift lässt
sich auch inhaltlich deuten: Der Telefonierzeit
sind die dabei entstehenden Kosten zugeordnet.
|
|
|
|
|
|
Zuordnungsvorschrift
|
|
Wird für beliebige Zahlen einer Definitionsmenge
die Variable x eingeführt und genutzt, dann
lassen sich die beiden zuvor beschriebenen Vorschriften
(Zuordnungen) wie folgt schreiben:
|
| |
|
|
| |
|
Bei diesen Zuordnungen
wird aber von den Größen nur die Maßzahl
betrachtet. Sie sind also eine Abstraktion von den
realen Bedeutungen. |
| |
|
|
|
Funktionsterm
|
|
Die Zuordnungen stecken
nunmehr als Rechenvorschrift in den beiden Termen
x² und 15 +
0,4·x, wobei für x alle Zahlen
aus einer vorgegebenen Definitionsmenge eingesetzt
werden können. Durch diese Terme wird
jedem x aus der Definitionsmenge genau ein Termwert
/ Funktionswert zugeordnet. Bei diesen beiden Zuordnungen
handelt es sich also um Funktionen. Daher
werden solche Terme auch Funktionsterme
genannt. |
| |
|
|
|
Darstellung
der Funktionen in einer Wertetafel
Wertetafeln stellen immer nur eine endliche Teilmenge
der Funktion dar, da die Definitionsmenge die
Menge der natürlichen Zahlen Na ist.
|
|
|
x —> x²,
x ε Na
|
|
x
|
x²
|
|
1
|
1
|
|
2
|
4
|
|
3
|
9
|
|
...
|
...
|
|
|
|
x —>
15 + 0,4 · x, x ε
Na
|
|
x
|
15 + 0,4 ·
x
|
|
1
|
15,4
|
|
2
|
15,8
|
|
3
|
16,2
|
|
...
|
...
|
|
| |
|
|
|
|
|
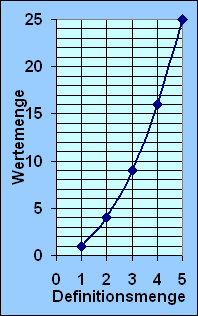
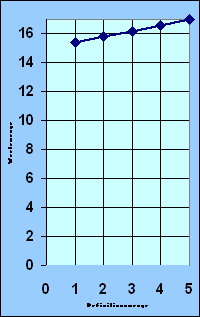
Veranschaulichung
der Funktionen in einem Liniendiagramm (in einem
Graph)
Auch Liniendiagramme veran-schaulichen nur eine
endliche Teilmenge der Funktion. Der Unterschied
zu vorher ist aber der, dass die Definitionsmenge
jetzt die Menge der rationalen Zahlen Ra ist.
Daher werden die Punkte des Diagramms jetzt durch
eine "Linie" miteinander verbunden.
|
|
 |
|
 |
| |
|
|
|
|
|
Funktionsgleichung
|
|
Häufig werden die Funktionsterme mit der
Variablen y oder f(x) bezeichnet. Wird die Definitionsmenge
mit dem Buchstaben D bezeichnet, so lassen sich
die vorstehenden Zuordnungsvorschriften auch als
Funktionsgleichungen wie folgt schreiben:
|
| |
|
|
|
|
| |
|
y = x²,
x ε D oder
f(x) = x², x ε D
|
|
y = 15 + 0,4 ·
x, x ε D oder
f(x) = 15 + 0,4 · x, x ε D
|
| |
|
|
|
|
| |
|
f(x) oder y heißen
dann für einen konkreten Wert x auch der Funktionswert
an der Stelle x. |
| |
|
|
|
Lösung
der Funktion
|
|
Jedes Zahlenpaar, das in die Funktionsgleichung
eingesetzt wird und sie zu einer wahren Aussage
macht, heißt Lösung der Funktion(sgleichung).
In den vorstehenden Wertetafeln, die zu den Funktionen
gehören, stehen Lösungen der jeweiligen
Funktion. Werden die Zahlenpaare der Wertetafel
in die jeweilige Funktionsgleichung eingesetzt,
so wird die Gleichung zu einer wahren Aussage.
Auch jeder Punkt auf den Graphen der Funktionen
ist eine Lösung. Denn wird das Zahlenpaar,
das zum Punkt gehört, in die jeweilige Funktionsgleichung
eingesetzt, so entsteht eine wahre Aussage. Funktionen,
die über N, Z, Ra oder Re definiert werden,
haben in der Regel unendlich viele Lösungen.
Der Graph der Funktion stellt jeweils die Lösungmenge
der Funktionsgleichung anschaulich dar.
|
| |
|
|
| |
|
|
| |
|
|
|
Exkurs:
Abstraktionen vom bedeutungsvollen Inhalt und
Erzeugung einer neuen,
"formalen" Realität
|
|
In der ("reinen") Mathematik werden
bei Abhängigkeiten zwischen Größen
nur die Maßzahlen der Größen
in Zusammenhang gebracht. Es werden also nur natürliche,
ganze, rationale und reelle Zahlen in Zusammenhang
gebracht. Das ist aber eine Abstraktion von dem
bedeutungsvollen Inhalt, der an den Größen
hängt.
(im Aufbau)
Durch diese Abstraktion entsteht ein neuer,
eigenständiger Inhalt - eine neue Realität
- nämlich die der Analysis. Sie wurde von
Newton und Leibniz, quasi gleichzeitig, erfunden.
Insbesondere für Newton hatte sie aber einen
ganz bestimmten Zweck, denn er wollte Bewegungsabläufe
besser verstehen. Heute wird die Analysis häufig
zweckfrei, gewissermaßen als mathematischer
Selbstzweck, unterrichtet.
Die abstrakte Analysis ist eine eigenständige
"Sprache" mit eigener Semiotik (Lehre
von den Zeichen), Syntax (Lehre vom Satzbau) und
Semantik (Lehre von der Bedeutung). Es ist eine
Metasprache, mit der Abhängigkeiten in Naturwissenschaft
und Technik, in Sozialwissenschaft und Politik,
in Ökonomie (Wirtschaft) und Finanzen, in
Medizin und Sport beschrieben werden können
und so in ihren wesentlichen Zusammenhängen
klarer erkannt und besser verstanden werden können.
So werden gewissermaßen "Stellschrauben"
deutlich, an denen gedreht werden könnte,
um die Welt human- und sozialverträglicher
zu gestalten.
Zu diesem Zweck muss die abstrakte Aussage der
Analysis immer wieder in die uns umgebende Realität
zurück interpretiert werden. Sie muss wieder
mit Leben gefüllt werden. Aus reinen Zahlen
müssen wieder Größen werden!
(im Aufbau)
|
|
|
|
|
|
|
|
|
 |
|
Letzte
Änderung:
15.10.2013
© Pädagogisches Institut für die deutsche Sprachgruppe
- Bozen. 2000 -
|
|
|














