Hackenberg Linus
Donnerstag, 21. Juli 2016
|
|
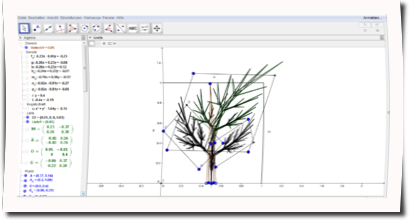
Der Tag wurde für das Design einer zur Veranschaulichung der Begründung für die These, dass die Anzahl von Spiralen immer eine Fibonacci-Zahl ist, verwendet. Die Steuerung erlaubt eine Veränderung von Winkel und der linearen Teile des Wachstums (es wird ein Tannenzapfen dargestellt) sowie einiger graphischer Elemente. Zudem wurden erste Teile der Präsentation mit der Präsentations-Software Prezi gestaltet.
|
Hackenberg Linus
Donnerstag, 21. Juli 2016
|
|
Die These, dass die Zahl der gleichen Spiralen eine Fibonacci-Zahl ist, wurde wie folgt (vereinfacht) begründet:
{1. Der Goldene Winkel lässt sich im Unendlichen in dem Blätterkonfigurations-System überschneiden:
n1 * 360/ϕ2 = 360°*n2 + 360/ϕ2 | /360°
n1/ ϕ2 = n2 + 1/ϕ2 | * ϕ2
n1 = ϕ2*n2 + 1 | -1
n3 (n3 ε N, eine natürliche Zahl größer 0 bleibt bei Subtraktion von 1 natürlich) = ϕ2*n2 |/n2
r (rε R) = ϕ2
r = ((sqrt(5)+1)/2)2
r = (sqrt(5)+1)^2 + sqrt(5) + 0,25
r = 5 + 1 + 2sqrt(5) +sqrt(5) + 0,25
r = 6,25 + 3sqrt(5) }
2. ϕ ist mit größter Ungenauigkeit mit a/b zu nähern:
ϕ = 1 + (1/ϕ) (Induktiv zu begründen)
ϕ = 1 + (1/(1/(1/ϕ)))
ϕ = 1 + (1/(1/(1/(1/(1/[...])))))
Kleinste Quotienten im Restbruch sind bei nicht-rationalen Zahlen der Indikator für Ungenauigkeit bei Annäherung mit a/b. Da 1 den kleinsten möglichen Quotienten darstellt, ist ϕ am schlechtesten mit a/b angenähert. Somit ist der Goldene Winkel (mit Einbezug von 1.)derjenige, der bei gleicher Zahl an Umdrehungen im Blätterkonfigurations-System den größten Durchschnittswinkel zwischen zwei Blättern und somit die gerinste Überschneidung aufweist. Er ist evolutiv "am besten".
3. Verhältnis von Blätterzahl (x) zu Umdrehungen:
1/ϕ2=fFibonacci(x)/fFibonacci(x+2)
Nach einer Fibonaccizahl von Blättern (bzw. dieser Zahl + n, solange n<Fibonacci(x+1)) hat das Blatt Fibonaccizahl - 2 Umdrehungen gemacht.
4. Insgesamt
Nach 1. nähert sich der Gesamtwinkel nach n Blättern 360*n2 an, und zwar mit kleiner werdendem Abstand. Demnach wird nach einer Fibonaccizahl an Blättern (3.) der Winkel zum nächten Blatt kleiner. Dies wird als Spirale wahrgenommen.
|
Kämmerer Luca
Mittwoch, 20. Juli 2016
|
|
Am dritten Tag unseres Projektes beendigten wir die 2D Version unseres Farns, in GeoGebra, und begannen den Fortschritt des 3D Fraktals, welcher uns gestern verloren ging, wieder aufzuholen.
Bild im Programm:
Am Anfang des Tages hingegen bekamen wir eine Einführung in das Programm Prezi welches uns bei unserer Abschlusspresentation helfen sollte.
In Java machten wir auch einige Fortschritte und entfernten einige Bugs,doch eine genauere Beschreibung der oben genannten Fortschritte muss Niklas wohl auf einem weiteren Blogeintrag machen, da ich an diesen Arbeitsschritten kaum mitgearbeitet habe.
Luca Kämmerer
Team:Niklas Lanig, Luca Kämmerer
Edit: Hier noch eine Nahauffnahme des Farns, er sieht noch ein bisschen dreieckig aus, da wir noch nicht die optimale Grunform für unser Fraktal gefunden haben.

|
Kämmerer Luca
Dienstag, 19. Juli 2016
Zuletzt geändert:
Mittwoch, 20. Juli 2016
|
|
Am heutigen Tag verfolgten wir weiter die Erstellung von Fraktalen, mithilfe von mathematischen Formeln, in GeoGebra.
Und konnten dies auch in der zweiten Dimension(2D) abschließen, doch durch einen GeoGebra-Fehler verloren wir an die zwei Stunden Fortschritt.
Während ich nach diesem Rückschlag versuchte das Ganze in die 3 Dimension zu übertragen, arbeitete Niklas daran das Projekt in Java (einer Programiersprache) zu transferieren.
Team: Niklas Lanig,Luca Kämmerer
|
Augschöll Petra
Dienstag, 19. Juli 2016
|
|

|
Augschöll Petra
Dienstag, 19. Juli 2016
|
|
Auch heute haben wir unsere Forschungen zum Thema Bienenwaben fortgesetzt. Nach mehreren Versuchen haben wir es endlich geschafft, sechseckige Bienenwaben aus Wachs herzustellen. Dabei haben wir mit heißen Glasstäben die Zitterbewegung von Bienen simuliert.
Anschließend haben wir das 3D-Modell am Computer fertiggestellt und mit Karton vier möglichst naturgetreue Bienenwaben gebaut.
Danach haben wir unsere Lötkünste ausgepackt und wiederum mit Seifenblasen experimentiert (siehe Foto). Das Besondere daran ist, dass sich Dreiecke bilden, so wie auch die Bienenwaben ineinanderpassen.
Auch mit der Frage, ob Bienenwaben wirklich optimal gebaut sind, haben wir uns beschäftigt. Dazu mussten wir die Fläche von verschiedenen Modellen berechnen. Die optimale Höhe der Spitze haben wir mit Hilfe von GeoGebra herausgefunden. Das Ergebnis verraten wir erst bei der Abschlusspräsentation am Freitag! ;-)
Liebe Grüße
Lukas, LUkas, Johanna, Lisa, Christian und Petra
|
Augschöll Petra
Montag, 18. Juli 2016
|
|

Wenn man Bienenwaben sieht, denkt man an ein Sechseck. In Wirklichkeit steckt aber viel mehr dahinter. Zuerst haben wir die Bienenwaben untersucht, genau vermessen und am Computer rekonstruiert (Lukas). Danach haben wir herausgefunden, warum Bienen genau sechseckige Waben bauen: Ein regelmäßiges Sechseck hat bei gegebenem Volumen nach dem Kreis die kleinste Oberfläche, und das so, dass sie aneinanderpassen, ohne Platz zu verlieren. Daneben haben wir die Schmelztemperatur von Wachs bestimmt, mit Seifenblasen Bienenwaben nachgebaut und versucht, aus Wachs sechseckige Waben herzustellen.
Lukas, Lukas, Johanna, Lisa, Christian und Petra ;-)
|
Kämmerer Luca
Montag, 18. Juli 2016
|
|
Wir begannen unser Projekt damit, dass wir und als Ziel gesetzt hatten am Ende der Woche einen Farn mithilfe eines Programms generieren zu können.
Wieso einen Farn? Da Farn eine perfektes Beispiel für Selbstähnlichkeit ist(Selbstähnlichkeit im engeren Sinne ist die Eigenschaft von Gegenständen, Körpern, Mengen oder geometrischen Objekten, in größeren Maßstäben, d. h. bei Vergrößerung, dieselben oder ähnliche Strukturen aufzuweisen wie im Anfangszustand.Quelle:http://tinyurl.com/gr2sg3n).
Den ersten Schritt in diese Richtung haben wir heute schon gelegt, indem wir in GeoGebra damit angefngen haben leichte Fraktale, mithilfe von mathematischen Formeln, zu generieren.
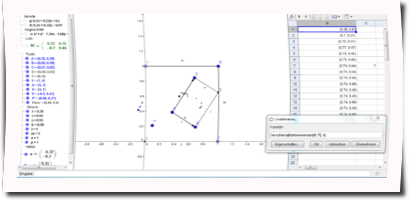 Autor: Luca Kämmerer Autor: Luca Kämmerer
Programmierteam:Niklas Lanig, Luca Kämmerer
|
Hackenberg Linus
Montag, 18. Juli 2016
|
|
Ausgehend von Spiralformen bei Tannenzapfen wurde zuerst ein Simulator für die Anordnung von Punkten in einem spiralförmigen System mit Einbezug der Fibonacci-Folge mittels GeoGebra programmiert.
Unter Verwendung der Hyphothese, die besagt, Pflanzen bildeten neue Blätter in konstantem Winkel zum letzten, wurde nach dem Winkel gesucht, der am wenigsten Überlagerung der Bätter verursacht und somit maximale Ausnutzung der natürlichen Umstände möglich macht. Wegen noch unbekannter Probleme war Geogebra nicht genau genung in der Lage, diesen Winkel mittels Pfadaufzeichnung aller möglichen Winkel (Element b/c*360°, b maximal 50, c maximal 50) zu verbildlichen.
|
Scherer Magdalena
Montag, 18. Juli 2016
|
|
von Magdalena, Joanna und Lea
Unser heutiger Tag begann mit der Ideenfindung für unser Wochenprojekt. Unsere Referenten zeigten uns zahlreiche Möglichkeiten auf aber ließen uns dennoch Freiraum für eigene Ideen. Wir befassen uns mit dem Schließmechanismus der Venusfliegenfalle und werden in den kommenden Tagen mehr davon berichten.
Versuch 1: Wir berühren die Venusfliegenfalle mit dem Stock mehrmals an einem einzigen der innen sitzenden und für das menschliche Auge sichtbaren Härchen.
Beobachtung: Schon bei der zweiten Berührung schließt sich die Falle. Es sind auf jeder Innenseite sind 4 Fühlborsten, die spiegelverkehrt angeordnet sind, zu finden. Je röter die Innenseite, also je älter der Teil der Pfanze ist, desto leichter und schneller reagiert sie auf die Berührungen. Bei grüneren Teilen der Pflanze sind zudem keine Fühlborsten mit dem bloßen Auge zu sehen, allenfalls ganz Feine.
Schlussfolgerung: Die wenigen (hier 8) innen sitzenden Fühlborsten sind der Auslöser für den Mechanismus der Pflanze.
Nun beschäftigen wir uns mit der Frage, ob ein verschieden großer zeitlicher Abstand zwischen den Berührungen einen Unterschied macht und ein zeitlicher Abstand allgemein überhaupt eine Rolle spielt.
Neue Frage: Warum frisst die Venusfliegenfalle ausgerechnet Fliegen?
Antwort: Wir haben die Antwort in dem Buch "Biologie der Pflanzen" gefunden. Es spielen einige Faktoren mit ein. Zuerst muss klargestellt werden, dass Venusfliegenfallen in sehr feuchten Gebieten, also Mooren leben. Jede Pflanze geht eine Symbiose mit Bakterien, die ihr bei der Aufnahme von Stickstoffverbindungen, die in für die Pflanze lebenswichtiges Phosphat oder Kalium umgewandelt werden, helfen. Da Moore einen saueren PH-Wert haben, sind die Lebensbedingungen für die helfenden Bakterien sehr schlecht. Deshalb ist dort nur eine sehr geringe Individuenzahl vorhanden und die Venusfliegenfalle muss die Stickstoffverbindungen von den Insekten aufnehmen. Zudem gibt es in Mooren viel leicht zersetzbares organisches Material für Bakterien, die Denitrifikation betreiben. Von diesen wird Nitrat aus dem Boden in gasförmigen Stickstoff umgewandelt, das in die Athmosphäre entweicht. Dadurch fehlt das Nitrat für die Pflanzen, für die dieses durch Mykorrhizapilze nutzbar gemacht werden kann. Auch die geringe Sonneneinstrahlung und Sauerstoffgehalt in Mooren lässt darauf schließen, dass die Venusfliegenfalle nicht genug Energie durch Fotosynthese erhält. Auf Grund dessen betreibt die Venusfliegenfalle nicht nur Fotosynthese, sondern frisst auch Insekten.
|



















 Autor: Luca Kämmerer
Autor: Luca Kämmerer
Kategorien:
Sommerakademie 2016Tag 3