Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung;
bezogen auf die Klassen 7 bis 10 (11) |
| |
|
|
Hinweise:
Die Bearbeitung der folgenden Aufgaben kann Teil einer Gesamtlösung von mehreren arbeitsteilig arbeitenden Kleingruppen sein.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben |
|
Die folgende Lösung zur Konstruktion und Simulation der Informationsweitergabe in einem hierarchischen Netz wird in einer Teilgruppe der Klasse erarbeitet. Sie ist Teil einer Gesamtlösung, bei der eine andere Gruppe der Klasse parallel arbeitet an der Konstruktion und Simulation einer "gebremsten" Informationsweitergabe in einem hierarchischen Netz. Wieder eine andere Gruppe arbeitet an der Konstruktion und Simulation eines "verzweigten" aber gerichteten Netzwerkes gegen akute Gewalt. Nach der Präsentation und Diskussion der Gruppenlösungen in der Klasse wird gemeinsam eine Aktionen erarbeitet.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 3 bis 4 Schulstunden notwendig, wenn auch Teilaufgaben zu Hause erledigt werden. Der Einsatz eines Werkzeugs z.B. Excel ist notwendig. Für eine Diskussion und Aktionsvorbereitung in der Klasse sind dann noch einmal 1 bis 2 Schulstunden notwendig.
|
|
|
|
|
|
Konstruktion und Simulation der Informationsweitergabe in einem hierarchischen Netz zur Solidarisierung gegen Gewalt |
| |
|
|
Konstruiert zunächst die beiden folgenden hierarchischen Netze: Im Netz A gibt ein Jugendlicher eine Nachricht an zwei und im Netz B an drei andere Jugendliche weiter. Und alle Informierte geben dann die Nachricht wieder an zwei bzw. drei andere weiter. usw.
Berechnet die Zahl der jeweils Informierten in einer Tabelle. |
|
Die folgende Tabelle zeigt die Anfangsberechnungen für die Weitergabe einer Information in einem hierarchischen Netz. Die Nachricht geht immer an alle alt und neu Informierte an zwei (Netz A) bzw. an drei andere (Netz B) Kinder oder Jugendliche weiter.
Runde
des
Weiter- sagens |
Netz A |
Netz B |
Faktor
des
Weiter-
sagens |
Anzahl
der Neu- Infor- mierten |
Anzahl
der
Infor- mierten |
Faktor
des
Weiter-
sagens |
Anzahl
der Neu- Infor- mierten |
Anzahl
der
Infor-
mierten |
0 |
|
0 |
1 |
|
0 |
1 |
1 |
2 |
2 |
3 |
3 |
3 |
4 |
2 |
2 |
6 |
9 |
3 |
12 |
16 |
usw. |
2 |
... |
... |
3 |
... |
... |
|
|
|
|
Konstruiert nun ein dynamisches Modell für die Weitergabe einer Nachricht in hierarchischen Netzen so, dass die Information zu Beginn auch von 2, 3, ... Jugendlichen ausgehen kann.
Beschreibt das Modell in Form eines Flussdiagramms
|
|
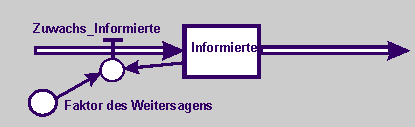
Die so berechnete Weitergabe einer Information lässt sich auch durch das folgende Flussdiagramms beschreiben. Wobei der Ausgang der Information von 2, 3 oder mehr Jugendlichen in diesem Modell die variable Anfangsgröße ist.
|
|
|
|
sowie in Form von
Zustands- und Modellgleichungen. |
|
Informierte_neu <-- Informierte_alt + Δt · Zuwachs_Informierte; Anfangsgröße = 1
Δt = 1 (1 Zeittakt = 5 Minuten)
Der Ausgang der Nachricht von 2 oder 3 oder mehr Kindern und Jugendlichen verbirgt sich in der Anfangsgröße.
Zuwachs_Informierte = Faktor_Weitersagen · Informierte
Faktor_Weitersagen = 2
|
| |
|
|
Programmiert die Zustands- und Modellgeichungen in einer Excel-Tabelle.
Simuliert unterschiedliche Ausbreitungen von Nachrichten und auch wie schnell alle Schülerinnen und Schüler einer Schule erreicht worden sind. |
|
Siehe hierzu:
ExcelDateien/Mappe1118a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1118a.xls (herunterladbar und interaktiv)
Sowohl die Anfangsgröße als auch der Faktor_Weitersagen werden abwechselnd um eine ganze Zahl erhöht.
In der Tabelle und auch im Punkt-Diagramm ist jeweils ablesbar, nach welcher Zeit alle Schüler und Schülerinnen einer Schule erreicht worden sind. Je größer die Anfangsgröße und je größer der Faktor_Weitersagen ist, um so schneller sind alle Kinder informiert.
Bei einer Anfangsgröße 3 und einem Faktor_Weitersagen 3 sind bereits nach 20 Minuten alle Kinder einer Schule mit ca. 600 Schülern und Schülerinnen informiert.
|
| |
|
|
| Diskutiert in eurer Kleingruppe, wie realistisch diese Netze sind. Denn beim Weitersagen treffen die Jugendlichen bereits nach einigen Runden auf andere, die schon darüber informiert sind, dass eine Aktion stattfindet. |
|
Bei den Simulationen des zuvor programmierten Modells gehen wir davon aus, dass diejenigen, die die Nachricht weitergeben, immer auf Jugendliche treffen, die noch nicht informiert sind. Das ist aber nach der zweiten oder dritten Runde bereits unwahrscheinlich. Das Modell ist also ein ideales Modell und nicht realistisch.
In den erneuten Modellierungen und Programmierungen werden wir zwei unterschiedliche Bremsmöglichkeiten berücksichtigen. |
|
|
|
|
|
Konstruktion und Simulation der gebremsten Informationsweitergabe in hierarchischen Netzen zur Solidarisierung gegen Gewalt |
| |
|
|
Konstruiert nun Modelle für die Weitergabe einer Nachricht, die unterschiedliche (unterschiedlich starke) "Bremsmöglichkeiten" bei der Ausbreitung berücksichtigt.
Beschreibt auch diese Modelle in Form eines Flussdiagramms.
|
|
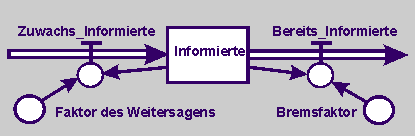
Modell 2: In diesem Modell wird angenommen, dass immer ein bestimmter (gleichbleibender) Anteil bereits informiert ist.
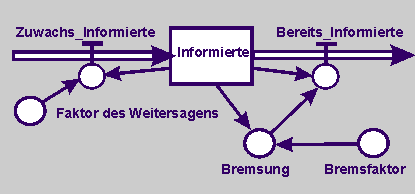
Modell 3: In diesem Modell wird angenommen, dass der Anteil der bereits Informierten mit der Zahl der Informierten steigt.
|
|
|
|
sowie in Form von
Zustands- und Modellgleichungen. |
|
Modell 2:
Informierte_neu <-- Informierte_alt + Δt · (Zuwachs_Informierte - Bereits_Informierte); Anfangsgröße = 1
Δt = 1 (1 Zeittakt = 5 Minuten)
Zuwachs_Informierte = Faktor_Weitersagen · Informierte
Bereits_Informierte = Bremsfaktor · Informierte
Faktor_Weitersagen = 2
Brems_Faktor = 0,5
Modell 3:
Informierte_neu <-- Informierte_alt + Δt · (Zuwachs_Informierte - Bereits_Informierte); Anfangsgröße = 10
Δt = 0,01 (1 Zeittakt soll = 1 Minute sein)
Zuwachs_Informierte = Faktor_Weitersagen · Informierte
Bereits_Informierte = Bremsung · Informierte_alt
Bremsung = Informierte_alt · Bremsfaktor
Faktor_Weitersagen = 2
Brems_Faktor = 0,002
|
|
|
|
Programmiert die Zustands- und Modellgeichungen in einer Excel-Tabelle.
Anmerkung: Zur Programmierung siehe: Crash-Kurse: Einführung in die Nutzung von Excel |
|
Zu Modell 2 siehe:
ExcelDateien/Mappe1118b1.htm (zur Ansicht) oder ExcelDateien/Mappe1118b1.xls (herunterladbar und interaktiv)
Zu Modell 3 siehe:
ExcelDateien/Mappe1118b3.htm ( zur Ansicht) oder ExcelDateien/Mappe1118b3.xls (herunterladbar und interaktiv)
|
|
|
|
Simuliert unterschiedliche starke Bremsungen und deutet sie.
|
|
Simulationen im Modell 2 zeigen, dass die Zahl der Informierten immer noch exponentiell steigt. Es dauert gegenüber dem ersten Modell nur etwas länger, bis alle Kinder oder Jugendlichen der Schule von der Nachricht erreicht werden. Das sagen auch die Funktionsvorschriften.
Simulationen im Modell 3 zeigen, dass sich die Zahl der Informierten einer oberen Grenze nähert. Der Zeittakt wurde in diesem Fall sehr klein gehalten und für Zahl der Informierten wurden Zahlen mit zwei Nachkommastellen zugelassen. So entsteht ein rechnerisch dichter (nahezu stetiger) Vorgang für die Weitergabe der Information. (Natürlich gibt es nur ganze Menschen.) Aber die obere Grenze hängt entscheidend vom Bremsfaktor ab. Bei einem starken Bremsfaktor werden nicht einmal alle Kinder und Jugendlichen der Schule erreicht. Wachstumskurven dieser Art heißen logistisch.
Wird aber im Modell 2 der Zeittakt auf 1 vergröbert und der Brems_Faktor mit 0,003 angenommen, so ergibt sich eine Kurve, die im maximalen Bereich hin und her schwankt.
Zu Modell 3 siehe:
ExcelDateien/Mappe1118b2.htm ( zur Ansicht) oder ExcelDateien/Mappe1118b2.xls (herunterladbar und interaktiv) |
| |
|
|
| In der nebenstehenden Excel-Mappe ist eine weitere Möglichkeit für eine Bremsung programmiert und beschrieben. |
|
Annahmen für ein weiteres gebremstes Weitergabemodell:
In diesem Weitergabemodell soll ab der 2. Runde die Zahl der Neu-Infizierten von der Rundenzahl linerar abhängig gemacht werden. Die Zahl der Informierten soll gebremst erscheinen. Simulationen für Δt zeigen aber schnell die Grenzen dieses Modells.
Siehe hierzu:
ExcelDateien/Mappe1118d.htm (zur Ansicht) oder ExcelDateien/Mappe1118d.xls (herunterladbar und interaktiv)
|
| |
|
|
| Organisiert zu gegebener Zeit an eurer Schule eine Aktion zur Solidarisierung gegen Gewalt unter Anwendung eines zuvor überlegten Netzes zur Weitergabe der Nachricht. |
|
Zu gegebener Zeit wird von einer Klasse ein hierarchisches Netz für die Weitergabe der Nachricht überlegt. Die Nachricht, die sich in der ersten Pause ausbreiten soll, lautet: "In der heutigen großen Pause versammeln sich alle Schülerinnen und Schüler der Schule in der Mitte des Schulhofs und schreien um Punkt 9,50Uhr fünfmal "Wir wollen keine Gewalt!". |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |















