Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung;
bezogen auf die Klassen (9) 10 bis 12 |
| |
|
|
|
|
|
Die folgende Lösung zum dynamischen Wachsen von Bevölkerungen kann in einer Teilgruppe der Klasse erarbeitet werden. Sie kann/sollte Teil einer Gesamtlösung sein, bei der andere Kleingruppen an Modell-Experimenten zum Wachsen von Bevölkerungen unter der Annahme von unterschiedlichen Bedingungen arbeiten.
Nach der Präsentation und Diskussion der Gruppenlösungen in der Klasse wird gemeinsam auch über den Sinn und Zweck dynamischer Modellierungen diskutiert.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 4 bis 5 Schulstunden notwendig, wenn auch Teilaufgaben zu Hause erledigt werden. Der Einsatz eines Werkzeugs z.B. Excel ist notwendig. Für eine Diskussion in der Klasse sind dann noch einmal 2 Schulstunden notwendig.
|
| |
|
|
|
|
|
|
|
Konstruktionen und Simulationen
zum dynamischen Wachsen von Bevölkerungen |
| |
|
|
Erstellt ein Wirkungsdiagramm zum Wachstum einer Bevölkerung |
|
 |
| |
|
|
| |
|
Bei Vernachlässigung der Größen Fruchtbarkeit und Sterbeziffer kann das Wirkungsdiagramm auch wie folgt aussehen: |
| |
|
|
| Erstellt für die ausgewählten Größen ein Wirkungsdiagramm. |
|
 |
| |
|
|
| Bestimmt nun die Zustands- und Flussgrößen sowie die Parameter, die ihr in diesem dynamischen Modell untersuchen wollt. |
|
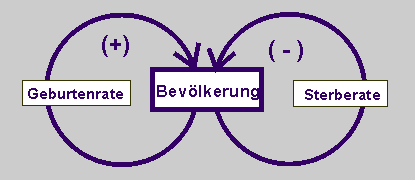
Das Wirkungsdiagramm besteht aus zwei Rückkopplungskreisen. Der eine ist positiv: Je mehr Menschen leben, umso mehr Kinder werden bei gegebener Geburtenrate geboren. Der andere Rückkopplungskreis ist negativ: Je mehr Menschen leben, umso mehr werden sterben, bei gegebener Sterberate.
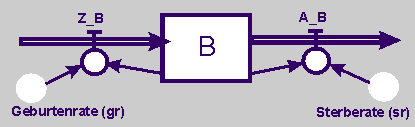
Es gibt also eine Zustandsgröße, die Bevölkerung (B). Auf diese wirken zwei Flussgrößen. Die Zunahme_Bevölkerung (Z_B) ist eine positive und die Abnahme_Bevölkerung (A_B) eine negative Rückkopplung. Die beiden Raten wirken ihrerseits auf die Flussgrößen. Mittels dieser Quantifizierung entsteht das folgende Flussdiagramm. |
| |
|
|
| Stellt sodann dieses Modell in einem Flussdiagramm dar. |
|
 |
| |
|
|
| Formuliert die Dynamik in Zustands- und Modellgleichungen und belegt die Größen mit Werten. |
|
B_neu <-- B_alt + Δt · (Z_B - A_B)
Anfangsgröße Bevölkerung B = 82218 (Deutschland im Jahr 2007);
Δt = 0,002; (1 Zeittakt = 1 Jahr)
Z_B = B · gr Λ A_B = b · sr
gr = 8,2 Λ sr = 10,7 (Deutschland im Jahr 2007) |
| |
|
|
| Programmiert das Modell mit Excel und simuliert das dynamische Modell. |
|
Siehe hierzu:
ExcelDateien/Mappe7660a.htm (nur zur Ansicht) oder ExcelDateien/Mappe7660a.xls (herunterladbar und interaktiv) |
| |
|
|
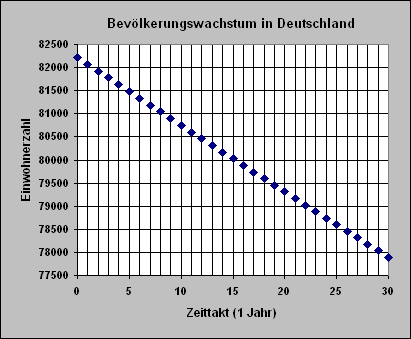
Wachstum der Bevölkerung in Deutschland ab dem Jahr 2007
in den nächsten 25 Jahren,
bei konstanter
Geburten- und Sterberate und
bei Δt = 0,002.
Bei diesem Zeittakt ergibt sich in 25 Jahren eine Bevölkerungszahl, die sich auch durch eine Hochrechnung bestätigen lässt. |
|
|
| |
|
|
| Erweitert das Modell zum Wachstum der Bevölkerung in Deutschland durch Eingabe von linearen Funktionen für die Geburten- und Sterberate. |
|
In das obige Modell werden nun für die Geburtenrate und Sterberate lineare Funktionen eingegeben, die durch eine Analyse der Bevölkerungdaten aus dem letzten Jahrzehnt gewonnen worden sind.
Die Geburtenrate gr = -0,1241x + 9,0966 nimmt ständig ab und
die Sterberate sr = 0,0397x + 10,058 nimmt ständig zu.
Siehe hierzu:
ExcelDateien/Mappe7660b.htm (nur zur Ansicht) oder ExcelDateien/Mappe7660b.xls (herunterladbar und interaktiv) |
| |
|
|
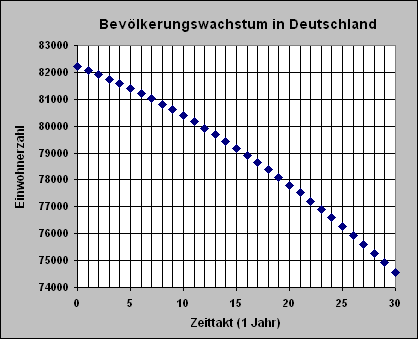
Wachstum der Bevölkerung in Deutschland ab dem Jahr 2007
in den nächsten 25 Jahren,
bei einer
Geburten- und Sterberate, die sich zeitabhängig linear verändern.
|
|
 |
| |
|
|
| Beschreibt und interpretiert in Worten das Systemverhalten, den Zweck und die Grenzen des Modells. |
|
Die Bevölkerung in Deutschland nimmt immer mehr ab. Und diese Abnahme beschleunigt sich sogar unter der Annahme, dass die Sterberate ständig größer und die Geburtenrate ständig kleiner wird. Deutschland ist also ein Land mit "aussterbender" Bevölkerung. In dem Modell blieb aber die Migrationsrate unberücksichtigt. Wird auch diese in das Modell mit einbezogen, bleibt die grundsätzliche Tendenz erhalten. |
| |
|
|
| Verschriftlicht eure Ergebnisse und erstellt eine Präsentation. |
|
Wesentliche Ergebnisse sind in den ExcelMappen dargestellt. Die Interpretationen sind im vorstehenden Text zu finden. |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |

















