|
|
|
|
|
|
| zur Analyse von Energieeffiziens am Beispiel der Kosten und des Energieumsatzes bei Glüh- und Energiesparlampen |
| |
Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung,
bezogen auf die Klassen 7 und 8 |
| |
|
|
Hinweise:
Die Bearbeitung der Aufgaben zur "Analyse von Energieeffizienz am Beispiel: Glühlampen - Energiesparlampen " ist Teil einer Gesamtlösung.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben |
|
Die folgende Lösung einer Analyse von Energieeffizienz
" im Privaten" am Beispiel: Glühlampen - Energiesparlampen wird in einer Teilgruppe der Klasse erarbeitet. Sie ist Teil einer Gesamtlösung, bei der andere Gruppe der Klasse parallel an Analysen von Energieeffizenz
"im Privaten" am
Beispiel: Stand-by oder am Beispiel: Haussanierungen arbeiten. Nach der Präsentation derGruppenlösungen in der Klasse werden gemeinsam Folgerungen erarbeitet, die auch das Verhalten von Menschen mit einbezieht.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 4 Schulstunden notwendig, wenn Teile dieser Arbeiten auch als Hausarbeit angefertigt werden. Für die Klassendiskussion ist dann noch einmal 1 Schulstunde notwendig. |
| |
|
|
|
|
|
|
|
Analyse von Energieeffizienz
" im Privaten" am Beispiel: Glühlampen - Energiesparlampen |
| |
|
|
Achtung: Glühlampen kann man in Deutschland nicht mehr kaufen. Heute wäre eher ein Vergleich von Halogen- oder Energiesparlampen mit LED-Beleuchtung sinnvoll. Die Überlegungen verlaufen ähnlich!
Kalkuliert mittels linearer Funktionen nach welcher Brennzeit eine teure Energiesparlampe kostengünstiger ist als eine billige Glühlampe.
Informiert euch zu diesem Zweck auch über die Energiekosten sowie über die Brenndauer von Energiesparlampen und Glühlampen.
|
|
Glühbirnen brennen rund 1.000 Stunden. Eine gängige Watt-Leistung liegt bei 60 Watt. Die Kosten pro Birne sind unterschiedlich. Einzeln kosten sie in der Regel ab 1€ aufwärts. In größeren Mengen sind sie auch billiger.
Hier wird ein 60 Watt Glühbirne angenommen, die 0,60€ kostet.
Energiesparleuchten haben eine durchschnittliche Brenndauer von bis zu 15.000 Stunden. Eine 11-Watt-Sparlampe leuchtet so hell wie eine normale 60-Watt-Glühbirne. Die Kosten für Energiesparlampen variieren, je nachdem wie viel Helligkeit gewünscht ist. Die einfachste Variante bekommt man schon ab 1€.
Hier wird eine 11-Watt-Sparlampe angenommen, die 2,90€ kostet. Weiter nehmen wir an, dass 1 kWh 15 Cent kosten.
Auf diesen Annahmen erstellen wir die folgende Tabelle zum Energie-Verbrauch und zu den Energie-Kosten, um so Glühlampe und Sparlampe miteinander vergleichen zu können.
Beispielrechnungen:
Der Energie(verbrauch) einer 60 W Glühbirne, wenn sie 100 h brennt berechnet sich wie folgt:
E = 60 W · 100 h
= 6000 Wh = 6 kWh
Wenn 1kWh 15 Cent kostet, dann kosten 6 kWh 90 Cent. Diese addieren sich zu den Anschaffungskosten von 60 Cent. Also:
100 h bei einer 60 W Glühlampe kosten 1,5 €.
Die anderen Werte in der folgenden Tabelle errechnen sich analog. Aber Achtung: Zu Beginn sind die Anschaffungskosten der Lampen zu berücksichtigen und nach 1000 Brennstunden eine Neuanschaffung von Glühbirnen.
Brenndauer
in h |
Energieverbrauch in kWh |
(Energie)-Kosten in € |
Sparlampe |
Glühlampe |
Sparlampe |
Glühlampe |
0 |
0 |
0 |
2,9 |
0,6 |
100 |
1,1 |
6 |
3,065 |
1,5 |
200 |
2,2 |
12 |
3,23 |
2,4 |
300 |
3,3 |
18 |
3,395 |
3,3 |
400 |
4,4 |
24 |
3,56 |
4,2 |
500 |
5,5 |
30 |
3,725 |
5,1 |
600 |
6,6 |
36 |
3,89 |
6 |
700 |
7,7 |
42 |
4,055 |
6,9 |
800 |
8,8 |
48 |
4,22 |
7,8 |
900 |
9,9 |
54 |
4,385 |
8,7 |
1000 |
11 |
60 |
4,55 |
10,2 (Sprung) |
1100 |
12,1 |
66 |
4,715 |
11,1 |
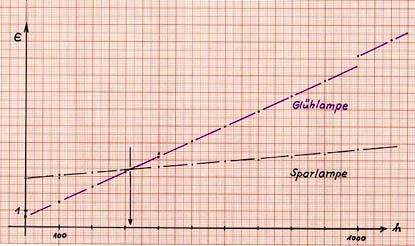
Die Abhängigkeit der Energiekosten in € von der Brenndauer in h werden als Punktdiagramme auf Millimeterpapier dargestellt. Es sind Geraden.
|
| |
|
|
| |
|
 |
| |
|
|
| |
|
Die Geraden sagen uns, dass nach etwa 310 h Brenndauer die Sparlampe günstiger ist, als die Glühlampe.
Das lässt sich aber auch berechnen. Dazu stellen wir zunächst mit Hilfe der Punkt-Steigungsform die linearen Funktionen für die Glühlampe (G) und für die Sparlampe (P) her:
y(G) = 0,9/100x + 0,6 und y(P) = 0,165/100x + 2,9
Für den Schnittpunkt der beiden Geraden gilt, dass y(G) = y(P) ist, daher:
0,9/100x + 0,6 = 0,165/100x + 2,9 äquivalent mit x = 312,925
Rechnerisch ist die Sparlampe nach 312,925 h Brenndauer günstiger als die Glühlampe.
|
|
|
|
Prognostiziert und diskutiert in eurer Kleingruppe eine mögliche Energieeinsparung
(a) in Deutschland und
(b) in Europa,
unter der Annahme, dass alle Haushalte die Glühbirnen in ihren Häusern durch Energiesparlampen ersetzen.
Was ist der Unterschied zwischen einer Extrapolation und einer Prognose? |
|
Unter einem Norm-Haushalt wollen wir hier verstehen, dass im ganzen Haushalt (1 Küche, 1 Bad, 1 Esszimmer, 1 Wohnzimmer, 2 Schlafzimmer) insgesamt 12 Glühlampen a 60 W oder 12 Sparlampen a 11 W brennen.
Wir nehmen weiter an, dass alle Lampen in diesem Normhaushalt im Jahresdurchschnitt etwa 2 h oder 4 h pro Tag brennen.
Die beiden Alternativen von 2 h oder 4 h Brenndauer je Lampe pro Tag dienen uns als eine wahrscheinliche Spannweite für die jährlichen Einsparungen. Auf dieser Basis prognostizieren wir bzw schätzen wir die jährlichen Energieeinsparungen.
Beispielrechnung:
12 · 60 W · 2 h = 1440 Wh = 1,44 kWh oder
12 · 11 W · 2 h = 264 Wh = 0,264 kWh
Tage |
Energie für 12 Glühlampen in kWh |
Energie für 12 Sparlampen in kWh |
Energieersparnis
in kWh |
2h/Tag |
4h/Tag |
2h/Tag |
4h/Tag |
2h/Tag |
4h/Tag |
1 |
1,44 |
2,88 |
0,264 |
0,528 |
1,176 |
2,352 |
2 |
2,88 |
5,76 |
0,528 |
1,056 |
2,352 |
4,704 |
... |
... |
... |
... |
... |
... |
... |
350 |
... |
... |
... |
... |
411,6 |
823,2 |
Im Jahre 2003 hatte Deutschland rund 82 Millionen Einwohner. Auf dieser Grundlage schätzen wir die Zahl der Normalhaushalte. Wir nehmen an, dass ein Normalhaushalt aus 4 Personen besteht, dann errechnen sich 20,5 Millionen Haushalte. Die auf dieser Grundlage abschätzbare Energieeinsparung in Deutschland pro Jahr wäre bei Sparlampen der Alternative 2h/Tag dann:
20500000 · 411,6 kWh = 8437800000 kWh
= 8437800 MWh = 8437,8 GWh = 8,437 TWh
Zum Vergleich: Ein Kohlekraftwerk mit einer installierten Leistung von 51,8 GW liefert pro Jahr bei 5810 h Einschaltdauer etwa 301 TWh Energie (siehe wikipedia). Das bedeutet unter den obigen Annahmen, dass in Deutschland ca. Eindreißigstel eines Kohlekraftwerkes eingespart werden könnte.
Besteht ein Normhaushalt aus 3 Personen, so wäre die abschätzbare Energieeinsparung in Deutschland pro Jahr bei Sparlampen der Alternative 4h/Tag:
27000000 · 823,2 kWh = 22221000000 kWh
= 22221000 MWh = 22221 GWh = 22,221 TWh
Ganz grob geschätzt könnte bei dieser Alternative etwa Einzehntel Kohlekraftwerk eingespart werden. Aber auf die Einwohnerzahl von 700 Millionen Einwohner in Europa hochgeschätzt könnte ein ganzes Kohlekraftwerk abgeschaltet werden.
Die vorstehenden Rechnungen sind eine Abschätzung - eine Prognose, die auf den zuvor gesetzten Annahmen beruhen. Gäbe es eine gesicherte Statistik zur Energieeinsparung durch Sparlampen, so könnte auf dieser Basis eine Funktion approximiert werden und mit ihr eine Extrapolation auf zukünftige Zeiten durchgeführt werden.
|
|
|
|
| Diskutiert in eurer Kleingruppe, ob dies ein wesentlicher Beitrag zur weltweit notwendigen Energieeinsparung sein kann. |
|
Resümee: Auf der Erde leben etwa 7000 Millionen Menschen. Das sind 10 mal so viel wie in Europa. Also könnten weltweit 10 Kohlekraftwerke abgestellt werden, wenn alle Glühbirnen durch Sparlampen ersetzt würden.
Und diese Zahl ist schon bewegender! Aber alleine durch Sparlampen lässt sich das Klimaproblem nicht lösen. Auch dies sagt diese Abschätzung.
|
|
|
|
| Verschriftlicht eure Ergebnisse und erstellt eine Präsentation. |
|
Wesentliche Ergebnisse sind in den ExcelMappen dargestellt. Die Interpretationen sind im vorstehenden Text zu finden.
|
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |
|
|
|













