Empirische Kovarianz
|
|
|
eingeführt am Beispiel |
|
|
des Merkmalspaares (Körpergröße/Gewicht)
von Jungen
 und und 
sind die Zeichen für die
arithmetischen
Mittelwerte einerseits für die Körpergröße x und andererseits für das Körpergewicht y,
oder auch m(x) und m(y).
Zum Verständnis der Rechnungen in nebenstehender und folgender Tabelle siehe:
Definition der empirischen Kovarianz
|
|
Index
i |
|
|
1 |
1,40 |
0 |
2 |
1,45 |
0,05 |
3 |
1,35 |
-0,05 |
4 |
1,39 |
-0,01 |
5 |
1,39 |
-0,01 |
6 |
1,30 |
-0,1 |
7 |
1,34 |
-0,06 |
8 |
1,44 |
0,04 |
9 |
1,38 |
-0.02 |
10 |
1,40 |
0 |
11 |
1,40 |
0 |
12 |
1,52 |
0,12 |
13 |
1,48 |
0,08 |
|
 ≈ 1,40308 ≈ 1,40 |
|
|
| |
|
|
| |
|
Index
i |
Gewicht Jungen
y |
|
|
|
1 |
33 |
-0,46 |
0 |
0 |
2 |
40 |
6,54 |
0,05 |
0,33 |
3 |
28 |
-5,46 |
-0,05 |
0,27 |
4 |
32 |
-1,46 |
-0,01 |
0,01 |
5 |
28 |
-5,46 |
-0,01 |
0,05 |
6 |
37 |
3,54 |
-0,1 |
-0,35 |
7 |
27 |
-6,46 |
-0,06 |
0,39 |
8 |
36 |
2,54 |
0,04 |
0,1 |
9 |
29 |
-4,46 |
-0.02 |
0,09 |
10 |
36 |
2,54 |
0 |
0 |
11 |
34 |
0,54 |
0 |
0 |
12 |
40 |
6,54 |
0,12 |
0,78 |
13 |
35 |
1,54 |
0,08 |
0,12 |
|
 ≈ 33,46145 |
|
|
Summe ≈ 1,79 |
|
|
|
|
Empirische Kovarianz s(xy) - Definition
Auf Grund nebenstehender Definition wird die empirische Kovarianz für das
Merkmalspaar (Körpergröße/Gewicht)
von Jungen berechnet.
|
|
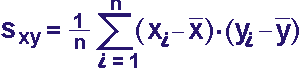
Es gibt ein vereinfachte Berechnung. Siehe hierzu die Gegenüberstellung der Berechnungen in der folgenden ExcelMappe.
s(xy) = m(x·y) - m(x)·m(y)
s(xy) ≈ 0,1386
|
| |
|
|
Excell-Mappe
zur Ansicht im Browser |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm..." öffnet sich im Browser eine Excel-Mappe zu Ansicht. Sie ist nicht interaktiv. Im Internet Explorer (ältere Version) kann sie mit "Datei öffnen mit Microsoft-Excel" in eine interaktive verwandelt werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Ansichtsseite schließt. |
Interaktive Excell-Mappe
im Browser öffnen |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm ... " öffnet sich im Browser ein Fenster zum Dateidownload. Mit "öffen" aktivieren und dann OK wird die Excel-Mappe geöffnet und ist interaktiv. Sie kann auch auf den eigenen Rechner geladen werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Excel-Mappe schließt. |
| |
|
|
Die empirische Kovarianz wird zur Beschreibung eines Zusammenhangs zwischen zwei Merkmalen herangezogen. |
|
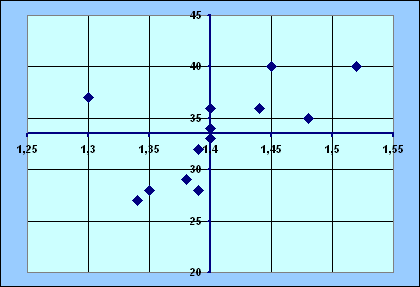
Das folgende Diagramm erklärt, warum die empirische Kovarianz einen Zusammenhang zwischen zwei Merkmalen beschreibt.
In diesem Diagramm liegt der Koordinatenursprung im Punkt [m(x)/m(y)]. Für alle Datenpunkte, die im ersten und dritten Quadranten liegen, sind die Produkte [ x(i) - m(x)] · [(y(i) - m(y)] positiv; also ist der Beitrag zur Kovarianz in der obigen Formel positiv. In diesem Fall finden sich bei großen Merkmalsausprägungen des Merkmals x auch große Ausprägungen des Merkmals y.
Für Daten im zweiten und vierten Quadranten ist der Beitrag negativ.
Also deutet ein positiver Wert der Kovarianz ein gleichsinniges Ordnungsverhalten der Merkmale an: Nehmen die Merkmalsausprägungen des Merkmals x zu, so nehmen auch die des Merkmals y zu.
Bei negativer Kovarianz kann von einem gegensinnigen Ordnungsverhalten gesprochen werden: Nimmt die Merkmalsausprägung x zu, so nimmt die des Merkmals y ab. |
| |
|
|
| |
|
 |
| |
|
|
ABER: Die empirische Kovarianz gibt lediglich einen Hinweis auf das gemeinsame Wachstumsverhalten der beiden Merkmale an. |
|
Die empirische Kovarianz gibt auf Grund des Vorzeichens einen Hinweis auf das gemeinsame Wachstumsverhalten der beiden Merkmale, sie erlaubt aber keine Aussage über die Stärke des Zusammenhangs. Aus diesem Grund wird eine Normierung so durchgeführt, dass das resultierende Maß - der Korrelationskoeffizient - immer zwischen 1 und -1 liegt. |
|
|
|
| |
|
Korrelationskoeffizient |
| |
|
|
Definition und Berechnung des Korrelationskoeffizienten
am Beispiel des Merkmalspaares
(Körpergröße/Gewicht)
von Jungen
|
|
Gegeben sei ein bivariates Merkmal (x/y) [etwa wie oben (Körpergröße x / Körpergewicht y) von Jungen], dann versteht man unter dem Korrelationskoeffizienten r(xy) den Qotient aus der empirischen Kovarianz s(xy) (siehe oben) und dem Produkt der Standardabweichungen s(x) und s(y).
r(xy) = s(xy) / s(x) · s(y)
r(xy) ≈ 0,574
Berechnung siehe folgende Excel-Tabellen |
| |
|
|
Excell-Mappe
zur Ansicht im Browser |
|
|
|
|
Mit Klick auf "Excel-Tabelle und -Diagramm..." öffnet sich im Browser eine Excel-Mappe zu Ansicht. Sie ist nicht interaktiv. Im Internet Explorer (ältere Version) kann sie mit "Datei öffnen mit Microsoft-Excel" in eine interaktive verwandelt werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Ansichtsseite schließt. |
Interaktive Excell-Mappe
im Browser öffnen |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm ... " öffnet sich im Browser ein Fenster zum Dateidownload. Mit "öffen" aktivieren und dann OK wird die Excel-Mappe geöffnet und ist interaktiv. Sie kann auch auf den eigenen Rechner geladen werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Excel-Mappe schließt. |
| |
|
|
Stärke und Interpretation
der Korrelation |
|
Die Merkmale x und y heißen
- schwach korreliert falls 0 ≤ |(r(xy)| ≤ 0,5
- stark korreliert falls 0,8 ≤ |(r(xy)| ≤ 1
Für unseren Fall der Körpergröße und des Körpergewichtes der 13 Jungen einer Grundschule heißt dies: Die Größen sind mäßig korreliert.
Im Streudiagramm erscheint in diesem Fall eine Punktwolke, die sich nur mäßig einer Geraden annähert. Wäre die Korrelation = 1 oder = - 1, so lägen die Punkte im Streudiagramm auf einer steigenden oder fallenden Gerade. Das wäre dann ein starker, linearer Zusammenhang. |
| |
|
|
  |
|
     |
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
- Die empirische Kovarianz lässt sich einfacher berechnen mit
s(xy) = m(x · y) - m(x) · m(y)
- Berechne die empirische Kovarianz von Körpergröße und Gewicht für die Mädchengruppe.
- Berechne den Korrelationskoeffizienten von Körpergröße und Gewicht für die Mädchengruppe.
- Leite die vereinfachte Formel für die empirische Varianz aus der Definitionsgleichung der Varianz her.
- Zeige, dass der Korrelationskoeffizient immer im Intervall [-1;1] liegt.
|












