blikk info infothek forum galerie sitemap

Schlussrechnen und lineare Funktionen
Zeit-Weg Abhängigkeit
am Beispiel für Züge von Adin nach Lamarin

anfang zurueck weiter ende nach oben

Bei allen Rechnungen handelt es sich um ein fiktives Fallbeispiel.
Bei den folgenden Wertetabellen wird angenommen, dass alle drei Züge mit einer konstanten Geschwindigkeit
von 60 km/h fahren.
  


Umrechnung für die Geschwindigkeit v = 60 km/h
     
 
Gegenzug1
Abf.:0.00 Uhr
in Adin
Gegenzug 2
Abfahrt: 4.00 Uhr
in Adin
Gegenzug 3
Abfahrt: 6.00 Uhr
in Adin
Ort
Kilometer - stein
Weg ( s )
in km
Zeit ( t ) in Minuten
Lamarin
0
80
80
320 (=80+240)
440 (=80+360)
Haluri
13
67
67
307 (=67+240)
427 (=67+360)
Gamin
24
56
56
296 (=56+240)
416 (=56+360)
Fiora
36
44
44
288 (=44+240)
404 (=44+360)
Emula
46
34
34
274 (=34+240)
394 (=34+360)
Dari
55
25
25
265 (=25+240)
385 (=25+360)
Chola
66
14
14
254 (=14+240)
374 (=14+360)
Belar
74
6
6
246 (=6+240)
366 (=6+360)
Adin
80
0
0
240 (=0+240)
360 (=0+360)
     
Umkehrgröße
zur Geschwindigkeit
  

     

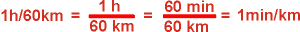
Schreibt ihr die vorstehende Wertetabelle so um, dass die Kilometersteine den zurückgelegten Weg angeben, dann ergibt sich die folgende Wertetabelle. Sie hat den Vorteil, dass alle
Zug-Geraden in dasselbe Koordinatensystem passen.

 
Gegenzug 1
Abf.:0.00 Uhr
in Adin
Gegenzug 2
Abfahrt: 4.00 Uhr
in Adin
Gegenzug 3
Abfahrt: 6.00 Uhr
in Adin
Ort
Weg (s) in km
Zeit ( t ) in Minuten
Lamarin
0
80 (= - 0+80)
320 (= - 0+320)
440 (= - 0+440)
Haluri
13
67 (= -13+80)
307 (= - 13+320)
427 (= - 13+440)
Gamin
24
56 (= - 24+80)
296 (= - 24+320)
416 (= - 24+440)
Fiora
36
44
288
404
Emula
46
34
274
394
Dari
55
25
265
385
Chola
66
14
254
374
Belar
74
6
246
366
Adin
80
0 (= - 80+80)
240 (= - 80+320)
360 (= - 80+440)
     
Zeit-Weg-Gleichungen
für Gegenzug 1, 2 und 3
  Vergleicht ihr nun die drei Zeit-Weg-Tabellen für Gegenzug 1, Gegenzug 2 und Gegenzug 3 miteinander, so ergeben sich zur Berechnung der Zeit (t) in Abhängigkeit vom Weg (s) die folgenden Zeit-Weg-Gleichungen:
     
Gegenzug 1
  
Gegenzug 2
  
Gegenzug 3
 
 
     
     

Liniendiagramme
zu den drei Gegenzügen

Auch bei den Diagrammen
wird angenommen, dass alle
drei Züge mit einer konstanten Geschwindigkeit von 60 km/h fahren.


Für die
Abfahrtzeit von Adin
nehmen wir an:

  • der erste Gegenzug 1
    fährt um 0.00 Uhr ab,
  • der zweite Gegenzug 2
    fährt um 4.00 Uhr ab und
  • der dritte Gegenzug 3
    fährt um 6.00 Uhr ab.



  
     
Bemerke!
  

Das Besondere dieser Darstellung ist, dass die Zeit-Weg-Diagramme in dasselbe Koordinatensystem wie vorher von Lamarin nach Adin eingezeichnet werden können.
Die Geraden fallen nun von links nach rechs ab: die Steigung der Geraden ist nun negativ! (in diesem Fall: -1min/km).
     
 
     
Ideen für mögliche, selbstorganisierte
Übungen:
 
  • Nutzt bei euren weiteren Experimenten das Werkzeug Excel. Die beiden folgenden Skizzen zur Erstellung einer Excel-Mappe können euch dabei helfen.
   
nach oben