Lineares Wachstum:
... geschrieben als
Menge geordneter Paare
|
|
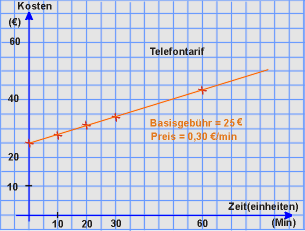
Die beiden voneinander abhängigen Größen bei Handytarifen bilden jeweils ein Paar, das auf folgende Weise geordnet ist: man nennt in dem Paar immer die unabhängige Größe t zuerst und dann die dazu berechnete, abhängige Größe. Beispiel:
Zeit (t) / Kosten (k): {(0/25), (10/28), (20/31), (30/34), ... (60/43) ...}
Den einzelnen (Zahlen)Paaren entsprechen die "Kreuze" auf der obigen linken Geraden. Aber zwischen diesen wenigen Kreuzen (Punkten) liegen noch (unendlich) viele weitere Punkte, die alle dieselbe Abhängigkeit beschreiben. Die Geraden beschreiben vollständiger als die Wertetabellen die Kosten-Zeit-Abhängigkeit. Diese Abhängigkeit lässt sich sich als Paarmenge mit einer Funktionsgleichung wie folgt schreiben:
{(t/k): k = 0,3€ · t + 25€} gelesen:
Menge aller Paare (t/k) für die gilt: k= 0,3€ · t + 25€ |
... geschrieben als
Zuordnung und Funktionsgleichung
|
|
Natürlich lässt sich die Kosten-Zeit-Abhängigkeit auch als Zuordung oder Funktionsgleichung schreiben:
s --> k, für k= 0,3€ · t + 25€
Für die unabhängige Variable (hier: t) muss die Definitionsmenge und für die abhängige Varible die Wertemege angegeben werden, für die die Funktionsgleichung bzw. die Zuordnung jeweils einen Sinn ergibt.
|