blikk info infothek forum galerie sitemap

Schlussrechnen und lineare Funktionen
Lineare Abhängigkeiten

 anfang zurueck weiter ende nach oben


Kosten/Menge-Abhängigkeit



Weg/Zeit-Abhängigkeit
 

Ihr habt bei der Arbeit an realen Problemen zum Beispiel die folgenden Abhängigkeiten kennengelernt.

Menge (item)
1
2
3
4
5
 ...
Kosten (US$)
39,94
79,88
119,82
159,76
199,70
 ...

Zeichnet ihr die die Wertepaare der Kosten/Menge-Abhängigkeit bei einem Preis von 39,94/item in ein Koordinatensystem ein und verbindet ihr die Punkte miteinander, so erhaltet ihr eine Gerade.

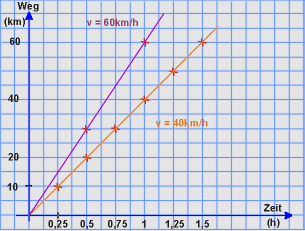
Zeichnet ihr die Wertepaare der Weg/Zeit-Abhängigkeit bei einer mittleren Geschwindigkeit von 40km/h oder 60km/h in eine Koordinatensystem ein und verbindet die Punkte miteinander, so erhaltet ihr zwei Geraden.

Zeit (h)
0,25
0,5
0,75
1
1,5
...
Weg (km)
10
20
30
40
60
...

     

Lineare Abhängigkeit:

geschrieben als
Menge geordneter Paare

 

  

Die beiden voneinander abhängigen Größen bilden jeweils ein Paar. Sie sind auf folgende Weise geordnet: man nennt in dem Paar immer die vorgegebene, unabhängige Größe zuerst und dann die berechnete, abhängige Größe. Lässt man die Maßeinheiten bei den Größen fort, so kann man die Abhängigkeiten auch als Mengen von geordneten Zahlenpaaren schreiben:

  • Menge/Kosten: {(1/39,94), (2/79,88), (3/119,82), (4/159,7), ...}
  • Zeit/Weg: {(0,25/10), (0,5/20), (0,75/30), (1/40), (2/60), ...}
     

geschrieben als
Paarmenge und Gerade

   Diese geordneten Zahlenpaare können als Punkte in ein geeichtes Koordinatensystem eingezeichnet werden. Auf der waagerechten Achse wird die unabhängige Größe und auf der dazu senkrechten Achse die abhängige Größe eingetragen. Zuvor müssen aber die beiden Achsen geeicht werden.
Alle Punkte der jeweiligen Paarmenge liegen auf einer Geraden. Den einzelnen (Zahlen)Paaren entsprechen jeweils die "Kreuze" auf den Geraden. Aber zwischen diesen wenigen Kreuzen (Punkten) liegen noch viele andere Punkte auf der Geraden, die auch alle genau dieselbe Abhängigkeit beschreiben.
     

geschrieben als
Funktionsgleichung

  

Die Geraden beschreiben also vollständiger als die Wertetabellen die Weg/Zeit-Abhängigkeit. Diese Abhängigkeit lässt sich sich als Paarmenge mit einer Funktionsgleichung wie folgt schreiben:

{(t/s): s = 40km/h · t} gelesen:
Menge aller Paare (t/s) für die gilt: s = 40km/h · t

Für die unabhängige Variable (hier: t) muss die Definitionsmenge und für die abhängige Varible die Wertemege angegeben werden, für die die Funktionsgleichung bzw. die Zuordnung jeweils einen Sinn ergibt.
     
Ergänzungen und Systematisierungen zur linearen Abhängigkeit
  
siehe auch: Lineares Wachstum
     
 
     
Ideen für mögliche, selbstorganisierte
Übungen:

Wenn es euch interessiert,
dann versucht einmal,
die eine oder andere der folgenden Aufgaben zu lösen.

 
  • Was ist das Besondere an den Geraden, die proportionale Größen darstellen?
    Was hat der Dreisatz mit der Proportionalität zu tun?
  • Eine Baufirma will eine Schutthalde abtransportieren. 2 Lkw könnten dies in 8 Stunden schaffen. Die Firma hat 2 Stunden Zeit. Wieviel Lkw braucht sie?
  • Für 15 Kühe reicht der Heuvorrat 20 Tage. Wie lange reicht der Vorrat für 18 Kühe?
  • Wenn zwei Größen umgekehrt proportional sind, wie verläuft dann der Graph? (siehe den umgekehrten Dreisatz!)
  • Erstellt für weitere selbstgewählte konstante Geschwindigkeiten Wertetabellen
    a) für den Weg in Abgängkeit von der Zeit und
    b) für die Zeit in Abhängigkeit vom Weg.
  • Erstellt ebenso für die von euch bevorzugten Handytarife (auch mit unterschiedlichen Grundgebühren) Wertetabellen.
  • Andere Tarife: Für den Internetzugang gibt es u.a. zwei Anbieter A und B.
    A verlangt einen Grundpreis von 5 € pro Monat sowie 2 Cent pro Minute
    B verlangt keinen Grundpreis dafür aber 5 Cent pro Minute.
    Welches der beiden Angebote ist für welche Fälle das günstigste?
  • Die Tabellen könnt ihr z.B. auch mit Excel herstellen. Mit den Rechenvorschriften oder Zuordnungsvorschriften oder Termen lassen sich die Wertetabellen ganz leicht "programmieren" bzw. erzeugen.
 
  • Auf einer 320 m² großen Fläche soll Rasen gesät werden. Ein 1,5kg Paket Rasensamen kostet 24,99 € und reicht für eine Fläche von 100 m². Wie viele Pakete werden gebraucht, wie viel kosten sie?
  • Welche Angebote sind jeweils die günstigten:
    Hackfleisch: 1,49€ / 250g oder 3,99€ / 1,5kg
    Kirschen: 4,99€ /1kg oder 2,59€ / 450g
  • Ein zylindrischer Glasbecher enthält 200 ml Flüssigkeit bei einer Flüssigkeitshöhe von 3 cm. Wie viel Flüssigkeit enthält der Becher bei einer Flüssigkeitshöhe von 5 cm, 7cm und 12 cm?
nach oben