|
Bestimmung des
Terms der
"Buro Creek Bridge"
|
|
|
| |
|
|
|
Hier die "abgelesene" Wertetabelle
|
|
|
x
|
0
|
5
|
7,6
|
9
|
|
y
|
0
|
- 1,8
|
- 4
|
- 6
|
|
| |
|
|
|
Die Frage lautet:
|
|
Wie könnt ihr mittels eines Terms
aus den vier x-Koordinaten 0; 5; 7,6 und 9 jeweils die dazu gehörigen
y-Koordinaten 0; -1,8; -4 und -6 errechnen? |
| |
|
|
|
Überlegungen
zu einer experimentellen Herleitung
des Terms
|
|
Erinnert
euch an den euch bekannten linearen Term m · x + b. Wenn
die Berechnungen mittels dieses Terms gelängen, dann wäre die Variable
b gleich Null, denn der Graph geht durch den Koordinatenursprung.
Wenn ihr jetzt mit diesem linearen Term experimentiert,
so werdet ihr nach einigem Probieren keine gut angenäherten y-Werte
finden.
Versucht es daher einmal mit dem Term a · x² + b. Auch hier muss die Formvariable b wieder Null sein, denn der
Graph geht durch den Koordinatenursprung (0/0). |
| |
|
|
| Excell-Mappe
zur Ansicht im Browser
|
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm..." öffnet sich im Browser eine Excel-Mappe zu Ansicht. Sie ist nicht interaktiv. Im Internet Explorer (ältere Version) kann sie mit "Datei öffnen mit Microsoft-Excel" in eine interaktive verwandelt werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Ansichtsseite schließt. |
Interaktive Excell-Mappe
im Browser öffnen |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm ... " öffnet sich im Browser ein Fenster zum Dateidownload. Mit "öffen" aktivieren und OK wird die Excel-Mappe geöffnet und ist interaktiv. Sie kann auch auf den eigenen Rechner geladen werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Excel-Mappe schließt. |
| |
|
|
|
Ein
mögliches Ergebnis des Experiments
|
|
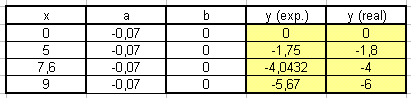
Nach einigen Zahlen-Einsetzungen
für die Formvariable a gelingt euch vielleicht die folgenden
Tabelle:
|
| |
|
|
|
Der
Term und die Funktionsgleichung
der Buro Creek Bridge
|
|
Der
Term mit dem aus den vier x-Koordinaten
0;
5; 7,6 und 9 jeweils die dazu gehörigen y-Koordinaten gut angenähert
errechnet werden können lautet also:
-
0,07 · x² + 0
Die
Funktionsgleichung lautet: y
= -
0,07 · x² + 0 |
|
|
|
|
|
Der
Term des "Ponto de Cecco"
|
| |
|
|
|
Zur Erinnerung die
"abgelesene" Wertetabelle
|
|
x |
- 5,7 |
0 |
1,8 |
5,7 |
7,2 |
y |
0 |
6,5 |
6,1 |
0 |
- 5,3 |
|
| |
|
|
|
Überlegungen
zur experimentellen Herleitung des Terms
|
|
Geht man bei
der folgenden experimentellen Herleitung wieder - wie zuvor beschrieben
- von dem Term a · x² + b aus, so lässt
sich durch Einsetzen der Null in diesen Term erkennen, dass die Formvariable
b gleich 6,5 ist. Der Graph geht durch den Punkt (0/6,5). |
| |
|
|
Excell-Mappe
zur Ansicht im Browser
|
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm..." öffnet sich im Browser eine Excel-Mappe zu Ansicht. Sie ist nicht interaktiv. Im Internet Explorer (ältere Version) kann sie mit "Datei öffnen mit Microsoft-Excel" in eine interaktive verwandelt werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Ansichtsseite schließt. |
Interaktive Excell-Mappe
im Browser öffnen
|
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm ... " öffnet sich im Browser ein Fenster zum Dateidownload. Mit "öffen" aktivieren und OK wird die Excel-Mappe geöffnet und ist interaktiv. Sie kann auch auf den eigenen Rechner geladen werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Excel-Mappe schließt. |
| |
|
|
|
Zwei
mögliche Ergebnisse
des Experiments
|
|
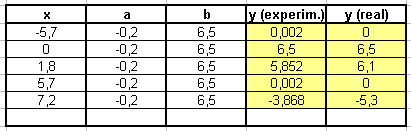
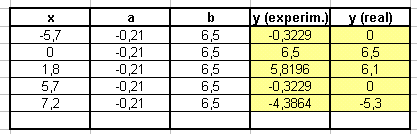
Nach einigem Experimentieren
werdet ihr vielleicht die beiden folgenden Tabellen finden. Die erste
ist - bis auf den Punkt (7,2/-5,3) - eine gute Annäherung an
den "realen" Bogen. Die Verzerrung beim Abstrahieren des
Bogens ist wohl noch nicht gut genug ausgeglichen worden.
|
| |
|
|
|
Der
Term und die Funktionsgleichung
des Ponto de Cecco
|
|
Der Term (die
Rechenvorschrift) mit dem aus den fünf x-Koordinaten -5,7;
0; 1,8; 5,7 und 7,2 jeweils die dazu gehörigen y-Koordinaten
gut angenähert errechnet werden können lautet also: - 0,2 · x² + 6,5
Die
Funktionsgleichung lautet: y
= - 0,2 · x² + 6,5 |
| |
|
|
|
Algebraische
Herleitung
des Terms
mit dem Werkzeug Derive
|
|
Die
mit Derive gefundene Funktionsgleichung lautet:
y = - 650/3249 x²
+ 13/2
oder:
y
= - 0,2000615 x² + 6,5
|
|
|
|
|
|
Der
Term der Autobahnbrücke in Hongkong
|
| |
|
|
|
Zur Erinnerung die
"abgelesene" Wertetabelle
|
|
|
x
|
- 2
|
0
|
2
|
4
|
6
|
8
|
|
y
|
0,6
|
0,2
|
0,6
|
1,9
|
3,9
|
6,4
|
|
| |
|
|
|
Ein
mögliches
experimentelles Ergebnis
mit Excel
|
|
Die experimentelle
Herleitung des Terms geschieht wieder - wie oben beschrieben - mit
dem Werkzeug Excel.
Nach einigem Experimentieren werdet ihr vielleicht die folgende Tabelle finden: 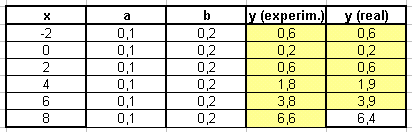 Der abstrahierte
Graph wird mit größer werdendem x zu flach. Auch hier könnte
die Verzerrung noch deutlicher beseitigt werden. Die experimentell
gefundenen Werte weisen den Weg für die Beseitigung der Verzerrung. |
Die Funktionsgleichung |
|
|
|
zur
Brücke
in Hongkong
|
|
Die Funktionsgleichung
lautet also: y
= 0,1 · x² + 0,2
|
|
|
|
|
|
Der
Term der Brücke "Espalion" |
| |
|
|
|
Zur Erinnerung die
"abgelesene" Wertetabelle
|
|
|
x
|
- 3,5
|
- 2
|
- 1
|
0
|
1
|
2
|
3,5
|
|
y
|
0
|
2,9
|
3,4
|
3,5
|
3,4
|
2,9
|
0
|
|
| |
|
|
|
Überlegungen
zu einer experimentellen Herleitung
des Terms
|
|
Für die Punkte
auf einem Kreis mit dem Radius r lässt sich die folgende Gleichung
aufstellen:
x² + y² = r²
y = Wurzel aus (r² - x²)
|
| |
|
|
|
Ein
mögliches
experimentelles Ergebnis
mit Excel
|
|
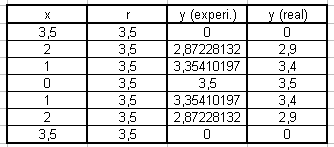
Mit dieser Formel
wurde die Exeltabelle programmiert. Die Ungenauigkeiten für y
(experi.) halten sich in diesem Fall im Rahmen von Ablesefehlern.
|
| |
|
|
|
Die
Funktionsgleichung zur
Brücke in Espalion
|
|
Die
Funktionsgleichung lautet also: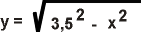 
|
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
- Abstrahiert von selbst gewählten weiteren Brückenbildern die Bögen sowie Wertepaare von ausgezeichneten Punkten und bestimmt den Term.
|
