Über-Lineares Wachstum:
... geschrieben als
Menge geordneter Paare
|
|
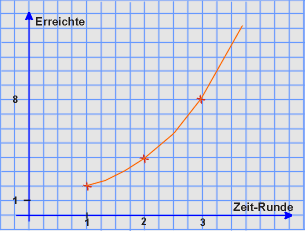
Die beiden voneinander abhängigen Größen beim Weitersagen bilden jeweils ein Paar. Es ist auf folgende Weise geordnet: man nennt in dem Paar immer die unabhängige Größe (den Zeittakt n) zuerst und dann die dazu berechnete, abhängige Größe.
Beispiel:
Zeittakt (n) / Erreichte (E): {(1/2), (2/4), (3/8), (4/16), ...(n/2^n) ..}
(2^n bedeutet: 2 hoch n)
|
... geschrieben als Funktionsgleichung
oder Zuordnung
| |
Das Wachstum des Weitersagens lässt sich als Paarmenge mit einer Funktionsgleichung vollständiger wie folgt schreiben:
{(n/E): E = 2^n}
gelesen:
Menge aller Paare (n/E) für die gilt: E = 2 hoch n
Natürlich lässt sich das Wachstum des Weitersagens auch als Zuordung oder Funktionsgleichung schreiben.
n --> E, für E =2^n
Für die unabhängige Variable (hier: Zeittakt n) muss die Definitionsmenge und für die abhängige Variable die Wertemenge angegeben werden, für die die Funktionsgleichung bzw. die Zuordnung jeweils einen Sinn ergibt.
|