Begrenztes Wachstum:
... geschrieben als
Menge geordneter Paare
|
|
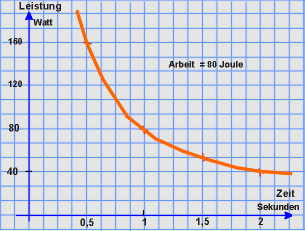
Die beiden voneinander abhängigen Größen bei der Zeit/Leistung Abhängigkeit bilden jeweils ein Paar. Es ist auf folgende Weise geordnet: man nennt in dem Paar immer die unabhängige Größe (die Zeit) zuerst und dann die dazu berechnete, abhängige Größe. Beispiel:
Zeit (t) / Leistung (P): {(0,5/160), (1/80), (1,5/53,33), (2/40), ...}
|
... geschrieben als
Paarmenge und Graph |
|
Diese geordneten Zahlenpaare können als Punkte in ein geeichtes Koordinatensystem eingezeichnet werden. Auf der waagerechten Achse wird die unabhängige Größe und auf der dazu senkrechten Achse die abhängige Größe eingetragen.
Der Graph für die Zeit/Leistung-Abhängigkeit ist eine Hyperbel (antiproportional oder umgekehrt proportional). Aber nicht alle Wachstumsgraphen für begrenztes Wachstum sind Hyperbeln (siehe oben links). Immer aber schmiegt sich der Graph bei zunehmender Zeit einer Parallelen zur waagerechten Achse an. Es gibt eine (obere oder untere) Schranke. |
... geschrieben als
Funktionsgleichung
und Zuordnung
|
|
Das Wachstum der Leistung P in der Zeit lässt sich als Paarmenge mit einer Funktionsgleichung vollständiger wie folgt schreiben:
{(t/P): P = 80J : t }
gelesen:
Menge aller Paare (t/P) für die gilt: P = 80J : t
Natürlich lässt sich das Wachstum der Leistung in der Zeit auch als Zuordung schreiben.
t --> P, für P = 80J : t
Für die unabhängige Variable (hier: t) muss die Definitionsmenge und für die abhängige Varible muss die Wertemenge angegeben werden, für die die Funktionsgleichung bzw. die Zuordnung jeweils einen Sinn ergibt.
siehe hierzu insbesondere:
Logarithmusfunktion - Systematisierungen |
|