Beispiel:
|
|
Die Kosten k eines Gutes stehen im funktionalen Zusammenhang mit der gekauften Menge m des Gutes; wobei der Preis p = 0,60€/1kg eine Konstante sein soll. |
| |
|
|
Die Lösungsmenge der Funktionsgleichung
k = 0,6€/1kg · m
als Wertetabelle
und vollständig
|
|
Menge (kg) |
0 |
0,25 |
0,5 |
0,75 |
1 |
1,5 |
2 |
... |
Kosten (€) |
0 |
0,15 |
0,30 |
0,45 |
0,60 |
0,90 |
1,20 |
... |
Die komplette Lösungsmenge der Funktionsgleichung lautet: {(m/k) / k = 0,6€/1kg · m} m ist irgendeine positive Zahl
|
| |
|
|
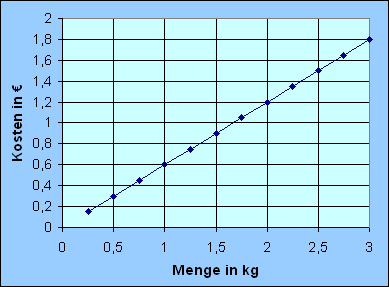
Darstellung
der Lösungsmenge als Graph im Koordinatensystem |
|
Die geordneten Wertepaare in obiger Wertetabelle können als Punkte in ein Koordinatensystem aus einer geeichten horinzontalen und vertikalen Achse eingetragen werden.
Den Schnittpunkt der beiden Achsen eines Koordinatensystems nennt man Koordinatenursprung.
Von hier aus gesehen entspricht z.B. dem geordneten Wertepaar (0,25/0,15) der Punkt: 0,25kg nach rechs und 0,15€ nach oben. Verkürzt spricht man vom Punkt (0,25/0,15). Die beiden Zahlen 0,25 und 0,15 nennt man die Koordinaten des Punktes. Aber auch bei den Koordinaten eines Punktes wird immer zuerst die unabhängige und dann die abhängige Größe angegeben.
Zwischen den Wertepaaren in der obigen Tabelle liegen jeweils noch unendlich viele. Sie werden veranschaulicht, wenn der Graph als Liniendiagramm durchgezeichnet wird.
|
| |
|
|
| |
|
|
| |
|
|
Ein wichtiger Hinweis
für folgende Abstraktionen |
|
In der Realität gibt es so gut wie keine abstrakten Zahlen, sondern nur Größen. In diesen tauchen die Zahlen als Maßzahlen auf. Und die kleinste, heute wirkliche Größe liegt in quantentheoretischer Größenordnung.
Die abzählbar, unendliche Menge der rationalen Zahlen und erst recht die überabzählbar, unendliche Menge der reellen Zahlen existiert als gedankliche Konstruktion bei Mathematikern. Diese Mengen und auch reellwertige Funktionen sind zwar in der mathematischen Wissenschaft hochinteressant, sonst aber ohne praktische Bedeutung!
Daraus folgt: In der Realität gibt es keine Funktionen, die überganz Re definiert sind. Es gibt nur Funktionen, die über einer endlichen Teilmengen der rationalen Zahlen stückweise definiert sind.
|
| |
|
|
Excell-Mappe
zur Ansicht im Browser |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm..." öffnet sich im Browser eine Excel-Mappe zu Ansicht. Sie ist nicht interaktiv. Im Internet Explorer (ältere Version) kann sie mit "Datei öffnen mit Microsoft-Excel" in eine interaktive verwandelt werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Ansichtsseite schließt. |
Interaktive Excell-Mappe
im Browser öffnen |
|
|
|
|
Mit Klick auf "Excel-Tabelle und -Diagramm ... " öffnet sich im Browser ein Fenster zum Dateidownload. Mit "öffen" aktivieren und dann OK wird die Excel-Mappe geöffnet und ist interaktiv. Sie kann auch auf den eigenen Rechner geladen werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Excel-Mappe schließt. |
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
- Macht die obige Exel-Tabelle interaktiv.
- Ändert sodann in der Exel-Tabelle den Wert für den Preis. Was geschieht dann?
- Zeichnet für die Funktionsgleichungen
I = a² und
s = 40km/1h · t
ebenfalls
einen Graph; siehe: Beispiele 2 und 3
- Nutzt dabei das Werkzeug Excel, wie es für das obige Beispiel vorgeführt wurde.
|
|
|
Das Mathematische Institut der Uni Wuppertal bietet interaktive Arbeitsblätter an, auf denen werden kann. U.a. gibt es Seiten Hyperbeln (antiproportionale Zuordnungen) und auch einige Seiten zu Quadratzahlen (Zahlenakrobatik). |
| |
|
|
|
|
mathe online Funktions-Plotter: Nach Eingabe einer oder mehrerer Terme werden die Grafen gezeichnet. Mit Hilfe der Zoom-Option können Grafen "aus der Nähe" betrachtet und die Koordinaten abgelesen werden.
|