|
Netze und dynamische Systeme
Bevölkerung, Nahrungsproduktion und Kapital - Beispiel: Subsahara-Zone |
|
 |
|
 |
|
 |
|
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Heute versuchen die führenden Industrieländer ihre technischen und gesellschaftlichen Strukturen neu zu gestalten und bemühen sich dabei, die ihnen innewohnenden Kräfte neu zu belegen und zu verjüngen, indem sie eine neue Qualität wirtschaftlichen Wachstums (Mehr unter Einsatz von
Weniger!) suchen. |
|
 |
| |
|
|
In den Ländern der Dritten Welt wird ein radikal anderer Weg verfolgt. |
|
"Da ihre schwachen wirtschaftlichen Kräfte ... noch immer kaum zur Befriedigung der Grundbedürfnisse ihrer schnell wachsenden Bevölkerungen ausreichen, setzen diese Länder gezwungenermaßen ihre Anstrengungen für quantitatives Wachstum fort. Auf diesem Weg wollen sie (z.B.) ... den Lebensstandard ihrer Bürger auf ein akzeptables Niveau heben, ihnen immer besseren Zugang zur Nahrung eröffnen,...“ (Eduard Pestel, 1988). |
| |
|
|
Wirkungsdiagramme |
|
Aus dem komplexen Wirkungsgefüge von "Bevölkerung, Kapital, Landwirtschaft und Umweltverschmutzung" (siehe Wirkungsdiagramme auf der Seite ma7655.htm#Untersuchung) werden nun die getrennten Subsysteme zum Bevölkerungswachstum, zur Nahrungsproduktion und zum Kapitaleinsatz in einen Wirkungsdiagramm und dann in folgendem Flussdiagramm vereint. |
| |
|
|
Flussdiagramm
des Wirkgefüges von Bevölkerungswachstum, Nahrungsproduktion und Kapitaleinsatz |
|
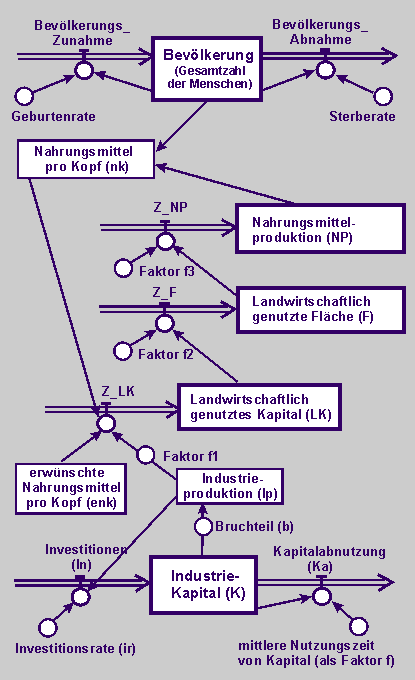 |
| |
|
|
Zustands- und Modellgleichungen mit Quantifizierungen für die Subsahara-Zone |
|
B_neu <-- B_alt + Δt · (Z_B - A_B)
Anfangsgröße Bevölkerung B = 750 Millionen (Subsahara-Zone);
Δt = 1; (Zeittakt = 1 Jahr)
Z_B = B · gr Λ A_B = b · sr
gr = 0,041 Λ sr = 0,029 (Mittelwerte Subsahara-Zone)
*************************************************************
LK_neu <-- LK_alt + Δt · Z_LK
Anfangsgröße landwirtschaftlich genutztes Kapital
LK = 600 Milliarden €;
F_neu <-- F_alt + Δt · Z_F
Anfangsgröße landwirtschaftlich genutzte Fläche
F = 300 Tausend ha;
NP_neu <-- NP_alt + Δt · Z_NP
Anfangsgröße Nahrungsproduktionsmenge
NP = 100 Mill. Tonnen;
Δt = 1 (Zeittakt = 1 Jahr)
Z_LK = (enk - nk) · f1 Λ F = LK · f2 Λ
Z_NP = F · f3 Λ nk = NP/ bz
enk = 0,26 Tonnen pro Jahr pro Kopf Λ
f1 = 8 Λ f2 = 0,016 Λ f3 = 0,015
***********************************************************
K_neu <-- K_alt + Δt · (In - Ka)
Anfangsgröße Kapital K = 2 Billionen €; Δt = 1; (Zeittakt = 1 Jahr)
In = Ip · ir Λ Ip = K · b Λ Ka = K · f
ir = 0,2 Λ b = 0,4 Λ f = 0,02 |
| |
|
|
Berechnung einiger Parameter
für die Zustands- und Modellgleichungen |
|
Der Hungerreport 2005 von"Brot für die Welt" spricht von Hunger, wenn die tägliche Energieaufnahme zwischen
1.400 und 1.800 Kilokalorien
pro Kopf pro Tag liegt.
Normal braucht ein Mensch rund 3000 kcal pro Tag. Das ist die Zielgröße in der folgenden Simulation. enk = 0,26 Tonnen Weizen pro Jahr pro Kopf entsprechen 0,72 kg pro Kopf pro Tag. Diese Menge entspricht rund 3000 kcal pro Kopf pro Tag, bei 1g Kohlenhydrate = 4,2 kcal.
Eine Nahrungsproduktion von
100 Millionen Tonnen (Weizen etc.) pro Jahr entsprechen rund
1500 kcal pro Kopf pro Tag.
(Das ist die gelbe Linie in der folgenden Simulation).
Hierzu siehe: ma0334a.htm#Situation |
| |
|
|
Programmierung der Zustands- und Modellgleichungen mit Excel |
|
Wir programmieren zunächst nur die vier Zustandsgleichungen für Bevölkerung, landwirtschaftlich genutztes Kapital, landwirtschaftlich genutzte Fläche und Nahrungsproduktionsmenge sowie die zugehörigen Modellgleichungen. Die Zahlen sind auf eine oder drei Stellen hinter dem Komma gerundet.
Die Faktoren f1, f2 und f3 sind experimentell so ermittelt, dass die verfügbare Nahrungsmenge pro Kopf steigt und sich aus der "Hungerzone" entfernt. Das ist die gewünsche Entwicklung in dieser Weltrregion.
Die Ausgangsgrößen entsprechen in etwa dem Zustand in der Subsahara-Zone (die insgesamt aus 48 Staaten besteht). Die Geburten- und Sterberate sind ein Mittelwert aus einigen dieser Länder und erzeugen eine Bevölkerungszahl, wie sie für 2020 in etwa von der Weltbank eingeschätzt wird.
In einer weiteren Programmierung könnte auch noch das Kapital einbezogen werden. Dies kann und sollte selbsorganisiert geschehen.
Siehe hierzu:
ExcelDateien/Mappe1328a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1328a.xls (herunterladbar und interaktiv) |
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen: |
|
Simuliert das Modell für die oben eingegebenen Größen. (Dann zeigt das Diagramm eine agrarbasierte Wachstumsstrategie, da in der Subsahara-Zone die Landwirtschaft der Schlüsselsektor für die volkswirtschaftliche Entwicklung und für die Reduzierung des Hungers ist. Er könnte noch schneller durch höheren Kapitaleinsatz reduziert werden.)
Simuliert das Modell unter den derzeitig vorherrschenden Verhältnissen, die zur Zeit noch durch eine starke Unterkapitalisierung gekennzeichnet ist. Daher setzt auf Grund von "bürgerkriegsartigen Querelen" in vielen dieser Staaten in der folgenden Simulation LK = 100 und F = 200. (Dann nimmt die Bevölkerung zwar auch weiter zu, aber der Hunger (die gelbe Linie) bleibt noch für sehr lange Zeit weit unter dem notwendigen Nahrungsbedarf von 3000 kcal pro Tag pro Kopf ! )
Siehe hierzu auch:
ExcelDateien/Mappe1328b.htm (nur zur Ansicht) oder ExcelDateien/Mappe1328b.xls (herunterladbar und interaktiv)
In einer dritten Simulationen nehmt an, dass durch "Aufklärung" die Geburtenrate gr = 0,041 stetig sinkt aber die Sterberate sr = 0,029 sich durch AIDS immer noch weiter erhöht. gr = -0,0001 · t + 0,041 und sr = 0,0001 · t + 0,029. (Dann ergeben sich auch bei schon bei niedrigerem Kapitaleinsatz LK = 300 aber gleich bleibend hoher Fläche F = 300 schon Verhältnisse, die den Hunger langsam beseitigen.)
Siehe hierzu auch:
ExcelDateien/Mappe1328c.htm (nur zur Ansicht) oder ExcelDateien/Mappe1328c.xls (herunterladbar und interaktiv)
|
|
|
|
|
|
|
|
|
|
Letzte Änderung: 09.02.2010
© Pädagogisches Institut für die deutsche Sprachgruppe
- Bozen. 2000 -
|
|
|
|
 |
|
|
|
|












