|
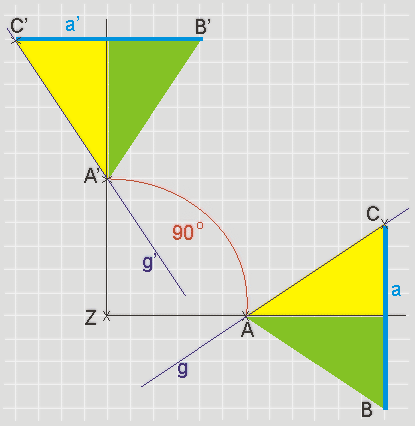
Gegeben ist ein Drehzentrum
Z und ein Drehwinkel
(in diesem Fall 90°).
Weiter sind gegeben: Ein beliebiger Originalpunkt
A und sein Bildpunkt A',
eine Originalgerade g und ihre Bildgerade g',
eine Originalstrecke a und ihre Bildstrecke a'.
|
|
 |
| |
|
|
|
Dann lassen sich für
die Drehsymmetrie die vier nebenstehenden Eigenschaften
finden und formulieren:
|
|
- Die Strecken [ZA] und [ZA'] sind gleich
lang. (Original- und Bildpunkt haben von Z den
gleichen Abstand.)
- Die Geraden ZA und ZA' bilden einen
Winkel miteinander, der gleich dem Drehwinkel
ist.
- Original- und Bildstrecken sind gleich
lang.
Es gilt: a = a'
- Originalgerade g und Bildgerade g'
schneiden sich und bilden einen Winkel miteinander,
der gleich dem Drehwinkel ist.
|
|
|
|
|
| |
|
|
|
Die Punktsymmetrie ist ein Spezialfall der Drehsymmetrie.
|
|
Zwei Figuren heißen punktsymmetrisch,
wenn der Drehwinkel 180° beträgt.
|
| |
|
|
|
|
|
|
| |
|
|
|
Ideen für mögliche,
selbstorganisierte
Übungen:
|
|
Gegeben sind ein beliebiges Dreieck ABC und ein
Drehwinkel.
- Konstruiert das Bilddreieck A'B'C' (siehe
die Figur oben).
- Zeigt an dieser Konstruktion die oben aufgezählten
Eigenschaften der Drehsymmetrie.
- Berechnet die Flächeninhalte von ABC
und A'B'C' und vergleicht sie miteinander. Könnt
ihr eine weitere Eigenschaft der Drehsymmetrie
vermuten?
- Wie müsst ihr euch drehen, wenn ihr in
ABC und A'B'C' den Buchstaben folgt? Ist der
"Drehsinn" in beiden Dreiecken der
gleiche? Gibt es einen Unterschied zur Achsensymmetrie?
|
|
|
|
|
|
Gegeben sind regelmäßige ebene Figuren,
wie unten in den Abbildungen.
- Wie viele Spiegelachsen haben ein Quadrat
und ein Rechteck?
- Wie viele Spiegelachsen haben ein gleichseitiges
Dreieck, Sechseck, Achteck ... ?
- Dreht man ein Quadrat um 0°, 90°,
180° und 270°, so kommt es
mit sich zur Deckung. Man spricht von einer
vierstrahligen Drehsymmetrie.
- Bei welchen Winkeln kommt ein Rechteck, eine
Raute, ein gleichseitiges Dreieck, Sechseck,
... mit sich zur Deckung?
|
|
|
|

|
|
|
|












