Ein Dreieck um einen Drehpunkt M um einen Winkel drehen

Voraussetzungen und Vorüberlegungen:

Das Originaldreieck ABC wird mit Hilfe des Geodreiecks oder eines Zirkels um einen Winkel gedreht.

Eigenschaften von Drehsymmetrien

Messen von Winkeln mit dem Geodreieck

Kreis und Zirkel - ein Zeicheninstrument

Mit einem Zirkel einen Punkt P um einen Drehpunkt M um einen Winkel drehen

Das Geodreieck ist notwendig, um den Drehwinkel zu zeichnen und die Länge der Abstände zu messen. Das Messen der Abstände geht auch mit einem Zirkel.


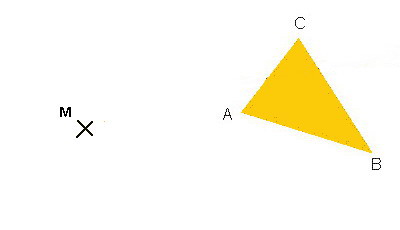
Erster Schritt: Gegeben sind ein Dreieck ABC und ein Drehpunkt M außerhalb von ABC. Das Ziel ist, das Dreieck ABC um einen Drehwinkel α um den Punkt M zu drehen.

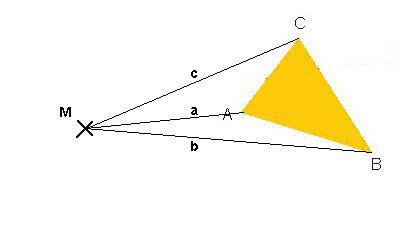
Zweiter Schritt: Es werden Geraden durch die Punkte M und C, M und A sowie M und B mit den Namen c, a und b angelegt.

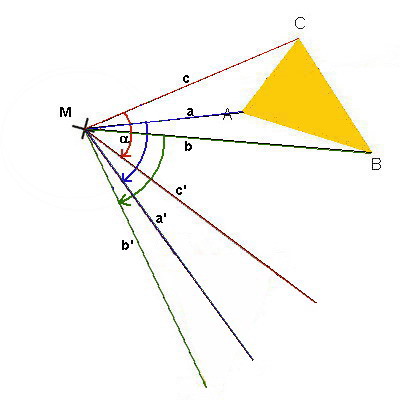
Dritter Schritt: An die Geraden c, a und b werden jeweils in M der gegebene Drehwinkel α angelegt. Dadurch enstehen die Hilfsgeraden c', a' und b'.

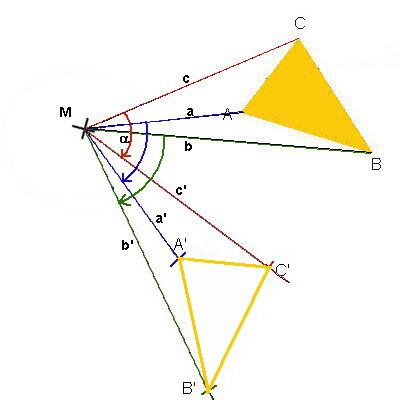
Vierter Schritt: Der Abstand MC auf c wird auf c' mit Hilfe eines Zirkels oder des Geogreiecks abgetragen. Dadurch entsteht C'. Ebenso entstehen die Punkte A' und B'.

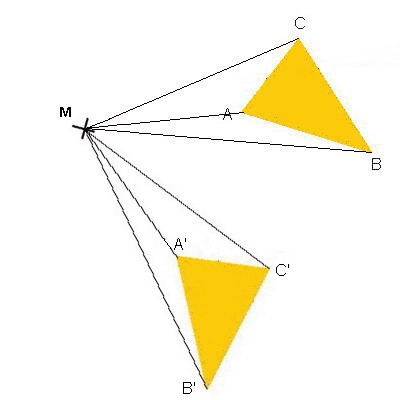
Fünfter Schritt: Das Dreieck A'B'C' ist das um den Drehwinkel α um den Punkt M gedrehte Dreieck.



Ideen für mögliche, selbstorganisierte Übungen:		Überlegt euch, welche möglichen Fehler bei der Konstruktion auftreten können. Messt die Seiten im Orginaldreieck und im Bilddreieck. Was fällt euch auf? Bleiben die Seitenlängen und Innenwinkel sowie der Umlaufsinn (Reihenfolge der Eckpunkte) des Dreiecks erhalten? Sind die Dreiecke ABC und A'B'C' deckungsgleich (kongruent)? Gebt ein beliebiges Rechteck ABCD vor und dreht es um 60° um einen beliebigen Punkt außerhalb des Rechtecks. Sind die Rechtecke ABCD und A'B'C'D' deckungsgleich (kongruent)?