|
|
|
|
|
|
|
|
|
|
|
Darstellung des Zusammenhangs von allgemeinen und inhaltsbezogenen
Kompetenzen sowie der Höhe der Anforderung - am Beispiel der
Sachsituation:
"Spiegelsymmetrien überall, auch an eurem Körper"
|
|

|

|

|

|

|
|
|
|
|
|
|
|
|
Grundlegende Erklärungen
zu allgemeinen und inhaltsbezogenen Kompetenzen
für den Primarbereich
|
|
Die allgemeinen und inhaltbezogenen Kompetenzen,
die für den Primarbereich (Jahrgangsstufe
4) in allen Bundesländern in Deutschland
am 15.10.2004 verbindlich vorgeschrieben wurden,
sind ausführlich formuliert unter:
|
|
|
|
|
|
Kompetenz
- Lernziel
|
|
Heute ist es üblich von allgemeinen
(oder prozessbezogenen) und inhaltlichen
Kompetenzen zu sprechen. Man spricht
nicht mehr von Lernzielen und von Lernzieltest
sondern von kompetenzorientierter Diagnose.
Aber auch der Begriff Kompetenz wird - wie früher
der Lernzielbegriff - auf den Grundbegriff
KÖNNEN zurückgeführt.
|
|
|
|
|
|
Allgemeine
und inhaltsbezogene Kompetenzen können weder
insoliert voneinander erworben noch diagnostiziert
werden
|
|
..."Das Mathematiklernen in der
Grundschule darf nicht auf die Aneignung von Kenntnissen
und Fertigkeiten reduziert werden. ...
Die Entwicklung von allgemeinen mathematischen
Kompetenzen hängt nicht nur davon ab, welche
Inhalte unterrichtet wurden, sondern in
mindestens gleichem Maße davon, wie sie
unterrichtet wurden, d. h. in
welchem Maße den Kindern Gelegenheit gegeben
wurde, selbst Probleme zu lösen, über
Mathematik zu kommunizieren usw. Die
allgemeinen mathematischen Kompetenzen sind mit
entscheidend für den Aufbau positiver Einstellungen
und Grundhaltungen zum Fach. In einem Mathematikunterricht,
der diese Kompetenzen in den Mittelpunkt des unterrichtlichen
Geschehens rückt, wird es besser gelingen,
die Freude an der Mathematik und die Entdeckerhaltung
der Kinder zu fördern und weiter auszubauen."
(siehe: Bildungsstandards Seite 6)
Und: Aufgaben sollen der Leistungsheterogenität
von Grundschülern dadurch Rechnung tragen,
dass sie im gleichen inhaltlichen Kontext
ein breites Spektrum an unterschiedlichen Anforderungen
und Schwierigkeiten abdecken. Dadurch
können die Aufgabenbeispiele zugleich als
Muster für einen differenzierenden Unterricht
fungieren, in dem alle Kinder am gleichen
Inhalt arbeiten, aber nicht unbedingt dieselben
Aufgaben lösen. (siehe Bildungsstandards
Seite 13)
|
|
|
|
|
|
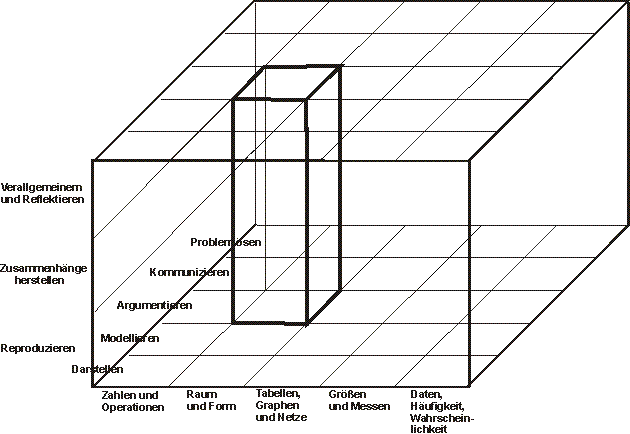
Darstellung
dieses Zusammenhanges in einem
"dreidimensionalen Raster"
|
|
Die "Dimensionen" für die Lernprozesse
der Kinder in einem "ganzheitlichen",
unterrichtlichen Angebot sind:
- Aneignung allgemeiner Kompetenzen
und gleichzeitig
- Aneignung inhaltsbezogener Kompetenzen
bei
- unterschiedlicher Höhe der Anforderung.
Alle drei Dimensionen realisieren sich im Rahmen
einer Sachsituation miteinander und zusammenwirkend.
Anders gesprochen: Im projektorientierten Unterricht
einer Sachsituation ist der Erwerb von inhaltlichen
und allgemeinen Kompetenzen miteinander und ineinander
verwoben. Und alle Kinder arbeiten am gleichen Inhalt,
lösen aber nicht unbedingt dieselben Aufgaben. |
|
Modelldarstellung
des Rasters
|
|
|
 |
| |
|
Betrachtung
des Zusammenwirkens beim Erwerb von allgemeinen
und inhaltsbezogenen Kompetenzen am Beispiel der
Sachsituation "Symmetrie ... "
|
|
Betrachten wir zunächst einmal etwas genauer,
wie der Erwerb allgemeiner und inhaltlicher Kompenzen
durch die "möglichen Anforderungen"
bei:
Wir untersuchen
(analysieren) Spiegel-Symmetrien und zeichnen
Spiegel"achsen"
angeleitet und angeregt wird. Diese Phase ist
mehr selbstreguliert. Und wie eine anschließende,
durch die Lehrperson moderierte Systematisierung
lokale, mathematische Ordnungen schafft. Diese
Phase ist mehr lehrgangsorientiert. Ihr schließt
sich abe wieder eine mehr selbstregulierte Phase
produktiven Übens an.
|
|
|
|
|
 |
| |
|
|
| |
|
Nummer
des Feldes
|
|
Mögliche
Anforderung
|
|
|
|
|
|
|
|
- Seht euch spiegelsymmetrische Flächen
und Körper aus dem von euch gewählten
Bereich an.
- Druckt sie aus und vergleicht sie miteinander.
Beachtet dabei die Verzerrung, die durch das
Foto entanden ist.
- Fotografiert oder skizziert spiegelsymmetrische
Figuren (Flächen und Körper) in eurer
Umgebung. Dann habt ihr noch mehr Material.
- Beschreibt mit euren eigenen Worten die Eigenschaft,
die alle diese Figuren (Flächen und Körper)
gemeinsam haben.
- Beschreibt die gemeinsame Eigenschaft mit
einer oder mehreren Geraden, die ihr in die
Figuren einzeichnet.
|
|
|
|
|
|
|
|
- Stellt einen Spiegel senkrecht auf die eingezeichnete(n)
Gerade(n), seht in den Spiegel und besprecht
miteinander, ob euch nun der Name Spiegelachse
verständlich wird.
- Ihr könnt eine (nahezu) achsensymmetrische
Figur auch durch Farb-Kleckse (u.a. mit Wasserfarben)
oder durch Falten und Ausschneiden selbst herstellen.
|
|
|
|
|
|
|
|
- Untersucht Dreiecke, Vierecke, ... Sechsecke,
... und Vielecke auf Achsen-Symmetrien.
- Zeichnet die Spiegel-Achsen in diese Grundfiguren
ein.
- Wie viel Spiegel-Achsen hat z.B. ein gleichseitiges
Dreieck oder ein gleichseitiges Sechseck?
- Untersucht Würfel, Quader, Pyramiden,
... und Kugeln auf Achsen- bzw. Flächen-Symmetrien.
- Bereitet zu allen euren Ergebnissen eine Präsentation
vor der Klasse vor.
|
|
|
|
|
|
|
|
- Diskutiert in eurer Kleingruppe, welche Bedeutung
Achsensymmetrie, Spiegelsymmetrie, Ebenensymmetrie,
Spiegel-Achse, Klapp-Achse und Spiegelebene
haben.
- Einigt euch auf Kriterien, nach denen ihr
die selbst hergestellten Achsen-Symmetrien bewerten
oder begutachten könnt.
- Begutachtet die von den anderen Kindern hergestellten
achsensymmetrischen Figuren nach den zuvor aufgestellten
Kriterien.
- Wie lassen sich "exakte"
Spiegelfiguren konstruieren?
- Bereitet zu allen euren Ergebnissen eine Präsentation
vor der Klasse vor.
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
Letzte
Änderung:
23.03.2013
© Pädagogisches Institut für die deutsche Sprachgruppe
- Bozen. 2000 -
|
|
|










