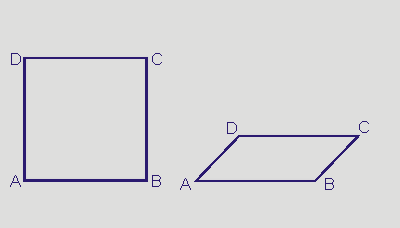
|
|
 |

|
|||||||||||||
 |
 |
 |
 |
|||||||||||||
Ein Schrägbild einer Pyramide |
|
|
|
|

|
||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| © Pädagogisches Institut für die deutsche Sprachgruppe Bozen 2000 - . Letzte Änderung: 22.05.2013 |  |