|
|
|
|
|
|
| |
|
|
Projektive Geometrie |
|
Projektive Geometrie bietet ein Hilfsmittel Punkte, Geraden, Ebenen, und Linien sowie Flächen zweiter Ordnung in einheitlicher Weise zu repräsentieren, etwa bei Landkarten.
Im Gegensatz zur euklidischen Geometrie können auch unendlich ferne Punkte und Geraden modelliert werden. Beispielsweise kann der Schnittpunkt zweier paralleler Geraden repräsentiert werden. |
| |
|
|
| |
|
|
| |
|
|
Darstellende Geometrie |
|
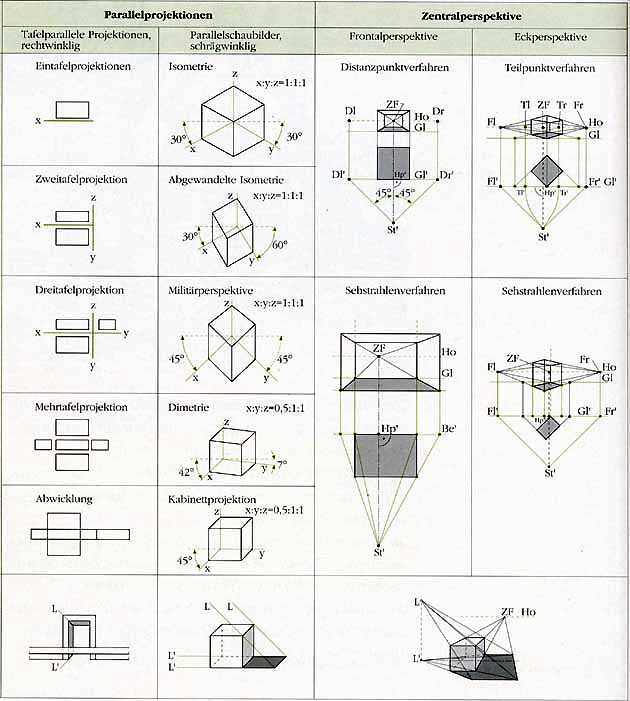
Die darstellende Geometrie beschäftigt sich mit der dreidimensionalen euklidischen Geometrie. Es wird u. a. untersucht, welche Eigenschaften die beiden Abbildungsmethoden der Parallelprojektion und Zentralperspektive (oder Zentralprojektion) haben, mit denen dreidimensionale Objekte auf eine zweidimensionale Bild- oder Tafelebene möglichst naturgetreu abgebildet werden können. Im Wesentlichen handelt es sich dabei um die Sätze der zentrischen Streckung und allgemeiner um die der Ähnlichkeitsabbildungen.
Lässt man bei der Zentralperspektive das Projektionszentrum "ins Unendliche" wandern, so ergibt sich die Parallelprojektion als Grenzfall der Zentralperspektive. Vom mathematischen Standpunkt aus ist daher nur diese intensiv zu untersuchen. Aber bereits seit dem ausgehenden Mittelalter haben sich zahlreiche Künstler und Mathematiker mit den Regeln der Zentralprojektion beschäftigt. Heutige Fotos bilden die dreidimensionale Wirklichkeit mittels Zentralprojektion ab.
|
| |
|
|
 |
| |
|
Übersicht aus: Baumgart / Müller / Zeugner:
Farbgestaltung; Baudekor - Schrift - Zeichnen, Cornelsen, 1996 |
| |
|
|
Tafelparallele Projektionen |
|
Tafelparallele Projektionen sind zweidimensionale rechtwinklige Darstellungen in Form von Schnitten, Ansichten und Abwicklungen. Sie geben die wahren Größen und Formen von Strecken, Flächen und Körpern maßstäblich wieder und sind daher für architektonische, baukonstruktiv-technische Vorhaben von großer Bedeutung. |
|
|
|









