| |
|
|
Koordinaten und Koordinatensystem
|
|
Mit Hilfe von Koordinaten lassen sich Punkte in einem Koordinatensystem durch Angabe von reellen Zahlen (auch Koordinaten genannt) eindeutig bestimmen. Mittels mehrerer Punkte lassen sich auch Geraden, Abstände, Ebenen und Körper angeben.
|
| |
|
|
Vektoren in der Ebene |
|
Gleichwertig zu Punkten ist der Ortsvektor des Punktes. Er stimmt mit den Koordinaten des Punktes (meist untereinander geschrieben) überein. |
| |
|
|
| |
|
|
| |
|
|
Vektoren
im dreidimensionalen (euklidischen) Raum |
|
|
| |
|
|
| |
|
Die Anzahl der zur Beschreibung notwendigen reellen Zahlen entspricht der Dimension des Raumes (oft als n abgekürzt). Man fasst die Koordinaten eines n-dimensionalen Raumes dann auch als ein n-Tupel von Koordinaten auf. Der Punkt, bei dem alle Koordinaten den Wert 0 annehmen, nennt man den Koordinatenursprung. |
| |
|
|
 |
|
Bei den Koordinatensystemen unterscheidet man zwischen geradlinigen (affinen) und krummlinigen Koordinatensystemen. Stehen die Achsen des Koordinatensystems aufeinander senkrecht (und sind beide Achsen gleich geeicht), so spricht man von einem kartesischen Koordinatensystem. Ein solches ist notwendig, wenn Abstände oder Winkel berechnet werden sollen.
Rene Descartes (1596 - 1650)
Als eine wichtige Entdeckung hat Descartes seine 'mathesis universalis' (Buchstabenalgebra) angesehen. Sie wurde von ihm als universale Grundlage aller Wissenschaften aufgefasst. Descartes ist der Wegbereiter der analytischen Geometrie, mit der er den entscheiden- den Schritt zur Einführung der mathematischen Formelsprache in die Physik ging. |
| |
|
|
Analytische Geometrie |
|
Die analytische Geometrie ist ein Teilgebiet der Geometrie, das algebraische Hilfsmittel zur Lösung geometrischer Probleme bereitstellt. Sie ermöglicht es in vielen Fällen, geometrische Aufgabenstellungen rein rechnerisch zu lösen. So können etwa die Schnittpunkte von Geraden oder der Schnittpunkt einer Geraden mit einer Ebene oder die Schnittgerade zweier Ebenen algebraisch bestimmt werden oder die Parallelität von Geraden oder Ebenen nachgewiesen werden.
Auch in der Physik und anderen Naturwissenschaften werden Verfahren der analytischen Geometrie eingesetzt, etwa bei der Beschreibung von Planetenbahnen.
|
| |
|
|
Beschreibung von Geraden
|
|
Geometrische Gebilde wie Geraden, Kreise usw. werden durch Vektor-Gleichungen beschrieben. Dabei handelt es sich heute in der Regel um Parametergleichungen wie etwa die folgenden für eine Gerade in der Ebene oder im Raum:
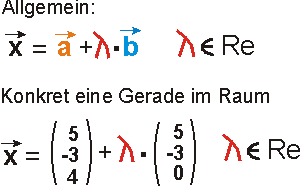 . .
|
| |
|
|
Beschreibung von Ebenen
|
|
Geometrische Gebilde wie Geraden, Ebenen, Kreise und Kugeln usw. werden durch Vektor-Gleichungen beschrieben. Dabei handelt es sich heute in der Regel zunächst um Parametergleichungen wie die zuvor ausgeführten.
|










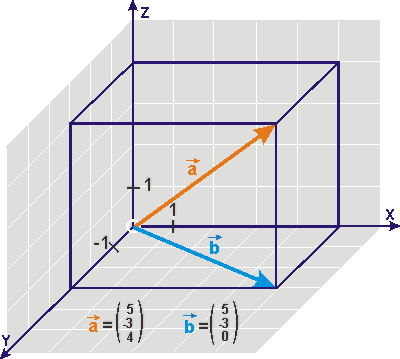

 .
.