|
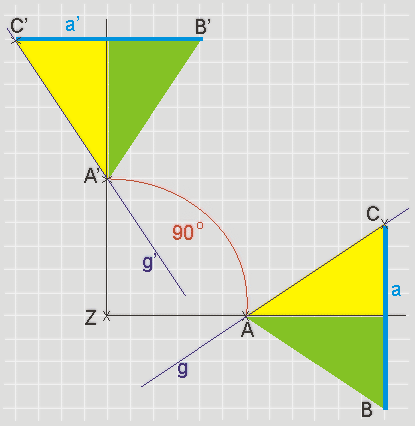
Dann lassen sich für
eine Drehsymmetrie die vier nebenstehenden Eigenschaften
finden und formulieren:
|
|
- Die Strecken [ZA] und [ZA'] sind gleich
lang. Original- und Bildpunkt haben von Z den
gleichen Abstand.
- Die Geraden ZA und ZA' bilden einen
Winkel miteinander, der gleich dem Drehwinkel
ist.
- Original- und Bildstrecken sind gleich
lang;
es gilt: a = a'
- Originalgerade g und Bildgerade g'
schneiden sich und bilden einen Winkel miteinander,
der gleich dem Drehwinkel ist.
|
|
Ideen für mögliche,
selbstorganisierte
Übungen:
| Dreieck:
Umfang und Flächeninhalt (in Arbeit)
|
|
|
Gegeben sei ein beliebiges Dreieck ABC und ein
Drehwinkel.
- Konstruiert das Bilddreieck A'B'C' (siehe
die Figur oben).
- Bestätigt an dieser Konstruktion die
oben aufgezählten Eigenschaften der Drehsymmetrie.
- Berechnet die Flächeninhalte von ABC
und A'B'C' und vergleicht sie miteinander. Könnt
ihr eine weitere Eigenschaft der Drehsymmetrie
vermuten?
- Wie müsst ihr euch drehen, wenn ihr in
ABC und A'B'C' den Buchstaben folgt? Ist der
"Drehsinn" in beiden Dreiecken der
gleiche? Gibt es einen Unterschied zur Achsensymmetrie?
Gegeben seien regelmäßige ebene Figuren,
wie unten in den Abbildungen.
- Wie viele Spiegelachsen haben ein Quadrat
und ein Rechteck?
- Wie viele Spiegelachsen haben ein gleichseitiges
Dreieck, Sechseck, Achteck ... ?
- Dreht man ein Quadrat um 0°, 90°,
180° und 270°, so kommt es
mit sich zur Deckung. Man spricht von einer
vierstrahligen Drehsymmetrie.
- Bei welchen Winkeln kommt ein Rechteck, eine
Raute, ein gleichseitiges Dreieck, Sechseck,
... mit sich zur Deckung?
|