Mehrstellige Zahl mal mehrstellige Zahl - Wie geht das?

Das Verfahren
(der Algorithmus) der schriftlichen Multiplikation natürlicher Zahlen wird in der Folge an einem Beispiel eingeführt und begründet.

Zerlegen von Multiplikations-Aufgaben

Das Verfahren wird an einem Beispiel gezeigt:

Begründung
des Verfahrens

  (300+50+6)·47
= 300·47+50·47+6·47
= 300·(40+7)+50·(40+7)
   +6·(40+7)
= 300·40 + 300·7 +
   50·40 + 50·7 + 6·40 + 6·7

= (300·40 + 50·40 + 6·40) +
(300·7 + 50·7 + 6·7)
= 14240 + 2492 = 16732

Die Aufgabe in
verkürzter Form ohne Stellenwertangabe

denn es gilt das Vertauschungsgesetz
(Kommutativgesetz)
der Addition
und
das Reihenfolgegesetz
(Assoziativgesetz)
der Addition

Mehrstellige Zahl mal einstellige Zahl
- Wie geht das?

Zweistellige Zahl mal zweistellige Zahl
- Wie geht das?

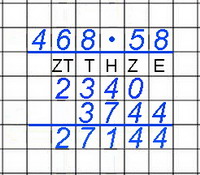
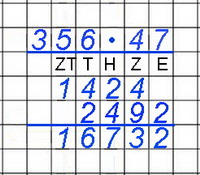
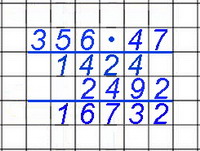
Ideen für mögliche, selbstorganisierte
Übungen:

Nutzt die Druckexemplare:

Leere Malstreifen
und
Rechnen in Malkreuzen

Erläutert in eurer Kleingruppe, wie ihr bei der letzten Multiplikation oben rechnen könnt.
Rechnet die beiden vorstehenden Multiplikationen auch im Malkreuz und mit Malstreifen.
Argumentiert an diesem Beispiel aber auch, warum ihr so rechnen dürft.
Gebt euch in eurer Kleingruppe nun gegenseitig schriftliche Multiplikationsaufgaben vor, wobei mehrstellige Zahlen mit mehrstelligen multipliziert werden sollen.
Führt das schriftliche Rechenverfahren aus.
Überprüft euch gegenseitig, indem ihr euch den Rechenverlauf vorsagt. Nutzt bei der Überprüfung eures Ergebnisses auch den Taschenrechner.